Question

【题目】如图，四棱锥中，为的中点．

求证：平面.

Answer 1

【答案】证明见解析

【解析】

试题分析：方法一，取PA的中点H，连接EH、DH。证明四边形DCEH是平行四边形，可得CE∥DH，根据线面平行的判定定理可得平面.

方法二：取AB的中点F，连接CF、EF，证明平面CEF∥平面PAD，可得平面.

试题解析：

方法一： 如图所示，取PA的中点H，连EH、DH.

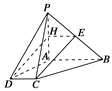
因为E为PB的中点，

所以EH∥AB，。

又AB∥CD，，

所以EH∥CD，EH＝CD.

因此四边形DCEH是平行四边形，

所以CE∥DH.

又DH平面PAD，CE平面PAD，

因此CE∥平面PAD.

方法二：如图所示，取AB的中点F，连CF、EF，

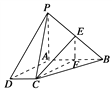
所以，又，

所以AF＝CD。

又AF∥CD，

所以四边形AFCD为平行四边形，

因此CF∥AD。

又CF平面PAD，AD平面PAD。

所以CF∥平面PAD。

因为E，F分别为PB，AB的中点，

所以EF∥PA。

又EF平面PAD，PA平面PAD，

所以EF∥平面PAD。

因为CF ∩ EF＝F，

所以平面CEF∥平面PAD。

又CE平面CEF，

所以CE∥平面PAD。