题目内容
7. 如图所示,几何体ABCDE中,△ABC为正三角形,CD⊥面ABC,BE∥CD,BC=CD=2BE.
如图所示,几何体ABCDE中,△ABC为正三角形,CD⊥面ABC,BE∥CD,BC=CD=2BE.(Ⅰ)在线段AD上找一点F,使EF∥平面ABC,并证明;
(Ⅱ)求证:面ADE⊥面ACD.
分析 (Ⅰ)取线段AC中点M,连结BM,FM,EF,证明出四边形BEFM平行四边形,推断出EF∥BM,进而利用线面平行的判定定理证明出EF∥平面ABC;
(Ⅱ)利用线面垂直的判定定理证明出BM⊥面ACD,进而推断EF⊥面ACD,最后利用面面垂直的判定定理证明出结论
解答 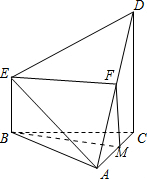 解:(Ⅰ)
解:(Ⅰ)
点F为线段AD中点,
证明如下:
取线段AC中点M,连结BM,FM,EF,
∵BE∥CD,BC=CD=2BE
则FM∥CD∥BE,且$FM=\frac{1}{2}CD=BE$,
所以四边形BEFM平行四边形,则EF∥BM,
又∵EF?平面ABC,BM⊆平面ABC,
∴EF∥平面ABC;
(Ⅱ)证明:∵△ABC为正三角形,
∴BM⊥AC,
∵CD⊥面ABC,BM⊆平面ABC,
∴CD⊥BM,
∵CD∩AC=C,
∴BM⊥面ACD,
∵EF∥BM,
∴EF⊥面ACD,
又EF⊆平面ADE,
∴面ADE⊥面ACD.
点评 本题主要考查了线面平行和面面垂直的判定定理的运用.考查了学生的一定的空间观察和想象能力.

练习册系列答案
相关题目
2.下列四个命题中正确命题的是( )
| A. | 学校抽取每个班级座号为21-30号的同学检查作业完成情况,这是分层抽样 | |
| B. | 可以通过频率分布直方图中最高小矩形的高来估计这组数据的众数 | |
| C. | 设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=1-p | |
| D. | 在散点图中,回归直线至少经过一个点 |
19.已知三棱锥S-ABC的所有顶点都在球O的表面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为( )
| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{2}}}{12}$ |
16.设x、y满足$\left\{\begin{array}{l}2x+y≥4\\ x-y≥-1\\ x-2y≤2\end{array}\right.$,则z=x+y( )
| A. | 有最小值2,最大值3 | B. | 有最大值3,无最大值 | ||
| C. | 有最小值2,无最大值 | D. | 既无最小值,也无最大值 |