题目内容
16．设x、y满足$\left\{\begin{array}{l}2x+y≥4\\ x-y≥-1\\ x-2y≤2\end{array}\right.$，则z=x+y（ ）| A． | 有最小值2，最大值3 | B． | 有最大值3，无最大值 | ||
| C． | 有最小值2，无最大值 | D． | 既无最小值，也无最大值 |
分析 作出不等式组对应的平面区域，利用目标函数的几何意义，求目标函数z=x+y的最小值．
解答 解：作出不等式组对应的平面区域如图：（阴影部分）．
由z=x+y得y=-x+z，平移直线y=-x+z，
由图象可知当直线y=-x+z经过点C时，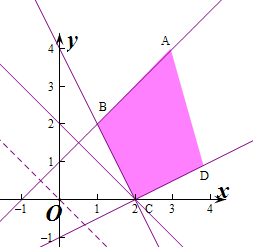
直线y=-x+z的截距最小，此时z最小．
由$\left\{\begin{array}{l}{2x+y=4}\\{x-2y=2}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$，即C（2，0），
代入目标函数z=x+y得z=2．
即目标函数z=x+y的最小值为2．
无最大．
故选：C．
点评 本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．
练习册系列答案
相关题目
如图所示，几何体ABCDE中，△ABC为正三角形，CD⊥面ABC，BE∥CD，BC=CD=2BE．
1．函数h（x）=2sin（2x+$\frac{π}{6}$），函数f（x）=2cos（2x-$\frac{2π}{3}$）可由h（x）经过（ ）的变换得到．
| A． | 向右平移$\frac{π}{6}$个单位 | B． | 向左平移$\frac{π}{6}$个单位 | ||
| C． | 向右平移$\frac{π}{3}$个单位 | D． | 向左平移$\frac{π}{3}$个单位 |
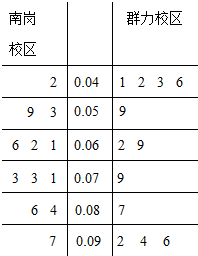PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据（单位：毫克/立方米）列出的茎叶图，南岗、群力两个校区浓度的方差较小的是（ ）