题目内容
17．已知函数f（x）=-x2+mx-n，m，n是区间[0，3]内任意两个实数，则事件f（1）＜0发生的概率为$\frac{7}{9}$．分析 由题意，本题是几何概型的考查，只要求出区域对应的面积，利用概率公式解答．
解答 解：函数f（x）=-x2+mx-n，m，n是区间[0，3]内任意两个实数，对应区间的面积为：9；
事件f（1）＜0对应的事件为-1+m-n＜0，在m，n是区间[0，3]内的前提下对应的区域如图
阴影部分，面积为9-$\frac{1}{2}×2×2$=7；
由几何概型公式得到事件f（1）＜0发生的概率为$\frac{7}{9}$；
故答案为：$\frac{7}{9}$．
点评 本题考查了几何概型公式的运用；关键是明确事件测度为对应区域的面积；利用面积比求概率．
练习册系列答案
相关题目
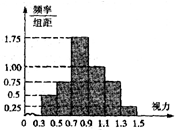某班50名学生的高校招生体检表中的视力情况进行统计，其结果的频率分布直方图如图所示．若A高校某专业对视力的要求在1.1以上，则该班学生中能报A高校该专业的人数为（ ）
如图所示，几何体ABCDE中，△ABC为正三角形，CD⊥面ABC，BE∥CD，BC=CD=2BE．