题目内容
19.已知三棱锥S-ABC的所有顶点都在球O的表面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为( )| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{2}}}{12}$ |
分析 根据题意作出图形,利用截面圆的性质即可求出OO1,进而求出底面ABC上的高SD,即可计算出三棱锥的体积.
解答 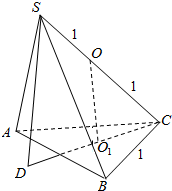 解:根据题意作出图形:
解:根据题意作出图形:
设球心为O,过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,
延长CO1交球于点D,则SD⊥平面ABC.
∵CO1=$\frac{2}{3}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}$,
∴OO1=$\sqrt{1-\frac{1}{3}}$=$\frac{\sqrt{6}}{3}$,
∴高SD=2OO1=$\frac{2\sqrt{6}}{3}$,
∵△ABC是边长为1的正三角形,
∴S△ABC=$\frac{\sqrt{3}}{4}$,
∴V三棱锥S-ABC=$\frac{1}{3}×\frac{\sqrt{3}}{4}×\frac{2\sqrt{6}}{3}$=$\frac{\sqrt{2}}{6}$.
故选:C.
点评 本题考查棱锥的体积,考查球内接多面体,解题的关键是确定点S到面ABC的距离.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
10.四面体ABCD的四个顶点均在半径为2的球面上,若AB、AC、AD两两垂直,$\overrightarrow{BA}•\overrightarrow{BC}$=2,则该四面体体积的最大值为( )
| A. | $\frac{7\sqrt{2}}{6}$ | B. | $\frac{7}{3}$ | C. | 2$\sqrt{2}$ | D. | 7$\sqrt{2}$ |
 如图所示,几何体ABCDE中,△ABC为正三角形,CD⊥面ABC,BE∥CD,BC=CD=2BE.
如图所示,几何体ABCDE中,△ABC为正三角形,CD⊥面ABC,BE∥CD,BC=CD=2BE.