题目内容
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 交于两点
交于两点![]() ,
,![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)把ρ=2sinθ两边同时乘以ρ,代入ρ2=x2+y2,y=ρsinθ即可得到曲线C的直角坐标方程;
(2)将直线l的参数方程![]() 代入圆的方程,化为关于t的一元二次方程,利用根与系数的关系化为关于α的三角函数,则答案可求.
代入圆的方程,化为关于t的一元二次方程,利用根与系数的关系化为关于α的三角函数,则答案可求.
解:(1)由ρ=2sinθ,得ρ2=2ρsinθ,
把ρ2=x2+y2,y=ρsinθ代入,可得x2+y2﹣2y=0.
∴曲线C的直角坐标方程为x2+y2﹣2y=0;
(2)将直线l的参数方程![]() 代入圆的方程,得t2+(2cosα﹣2sinα)t+1=0.
代入圆的方程,得t2+(2cosα﹣2sinα)t+1=0.
由△=(2cosα﹣2sinα)2﹣4>0,得sin2α<0,
且t1+t2=﹣2cosα+2sinα,t1t2=1.
∴![]() .
.
![]() sin2α<0∴
sin2α<0∴![]()
![]()
即![]() 的取值范围是(2,6].
的取值范围是(2,6].

练习册系列答案
相关题目
【题目】某小区为了了解业主用水情况,该小区分为一期和二期,入住共达4000户,现在通过随机抽样获得了100户居民的月均用水量,下图是调查结果的频数分布表和频率分布直方图.
分组 |
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 |
分组 |
|
|
|
| |
频数 | 14 | 6 | 4 | 2 |
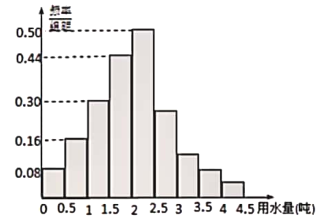
(1)估计该小区月均用水量超过3.8吨约有多少户;(2)通过频率分布直方图,估计该小区居民月均用水量平均值和中位数?