题目内容
【题目】已知函数![]() .
.
(I)若曲线![]() 存在斜率为-1的切线,求实数a的取值范围;
存在斜率为-1的切线,求实数a的取值范围;
(II)求![]() 的单调区间;
的单调区间;
(III)设函数![]() ,求证:当
,求证:当![]() 时,
时, ![]() 在
在![]() 上存在极小值.
上存在极小值.
【答案】(Ⅰ) ![]() .(Ⅱ)答案见解析;(Ⅲ)证明见解析.
.(Ⅱ)答案见解析;(Ⅲ)证明见解析.
【解析】试题分析:
(1)求出函数的导数,问题转化为![]() 存在大于
存在大于![]() 的实数根,根据
的实数根,根据![]() 在
在![]() 时递增,求出
时递增,求出![]() 的范围即可;
的范围即可;
(2)求出函数的导数,通过讨论![]() 的范围,判断导数的符号,求出函数的单调区间即可;
的范围,判断导数的符号,求出函数的单调区间即可;
(3)求出函数![]() ,根据
,根据![]() ,得到存在
,得到存在![]() ,满足
,满足![]() ,从而让得到函数单调区间,求出函数的极小值,证处结论即可.
,从而让得到函数单调区间,求出函数的极小值,证处结论即可.
试题解析:
(I)由![]() 得
得![]() .
.
由已知曲线![]() 存在斜率为-1的切线,所以
存在斜率为-1的切线,所以![]() 存在大于零的实数根,
存在大于零的实数根,
即![]() 存在大于零的实数根,因为
存在大于零的实数根,因为![]() 在
在![]() 时单调递增,
时单调递增,
所以实数a的取值范围![]() .
.
(II)由![]() 可得
可得
当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 的增区间为
的增区间为![]() ;
;
当![]() 时,若
时,若![]() ,
, ![]() ,若
,若![]() ,
, ![]() ,
,
所以此时函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() .
.
(III)由![]() 及题设得
及题设得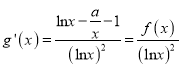 ,
,
由![]() 可得
可得![]() ,由(II)可知函数
,由(II)可知函数![]() 在
在![]() 上递增,
上递增,
所以![]() ,取
,取![]() ,显然
,显然![]() ,
,
![]() ,所以存在
,所以存在![]() 满足
满足![]() ,即存在
,即存在![]() 满足
满足![]() ,所以
,所以![]() ,
, ![]() 在区间(1,+∞)上的情况如下:
在区间(1,+∞)上的情况如下:
![]()
![]()
![]()
![]()
![]() - 0 +
- 0 +
![]() ↘ 极小 ↗
↘ 极小 ↗
所以当-1<a<0时,g(x)在(1,+∞)上存在极小值.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目

