题目内容
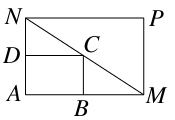
如图，已知小矩形花坛ABCD中，AB＝3 m，AD＝2 m，现要将小矩形花坛建成大矩形花坛AMPN，使点B在AM上，点D在AN上，且对角线MN过点C.
(1)要使矩形AMPN的面积大于32 m2，AN的长应在什么范围内？
(2)M，N是否存在这样的位置，使矩形AMPN的面积最小？若存在，求出这个最小面积及相应的AM，AN的长度；若不存在，说明理由．
(1)要使矩形AMPN的面积大于32 m2，AN的长应在什么范围内？
(2)M，N是否存在这样的位置，使矩形AMPN的面积最小？若存在，求出这个最小面积及相应的AM，AN的长度；若不存在，说明理由．
（1）在(2，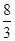
)或(8，＋∞)内
（2）AM＝6，AN＝4时，Smin＝24.
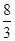)或(8，＋∞)内（2）AM＝6，AN＝4时，Smin＝24.
解：(1)设AM＝x，AN＝y(x>3，y>2)，矩形AMPN的面积为S，则S＝xy.
∵△NDC∽△NAM，∴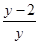
＝
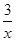，∴x＝
，
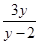∴S＝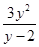
(y>2)．
由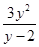>32，得2<y<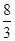，或y>8，
∴AN的长度应在(2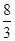，)或(8，＋∞)内．
(2)当y>2时，S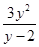＝＝3(y－2＋
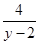＋4)≥3×(4＋4)＝24，
当且仅当y－2＝，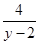
即y＝4时，等号成立，解得x＝6.
∴存在M，N点，当AM＝6，AN＝4时，Smin＝24.
∵△NDC∽△NAM，∴
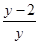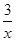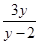＝，∴x＝，∴S＝
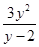(y>2)．由
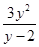>32，得2<y<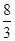，或y>8，∴AN的长度应在(2，
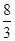)或(8，＋∞)内．(2)当y>2时，S＝
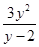＝3(y－2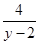＋＋4)≥3×(4＋4)＝24，当且仅当y－2＝
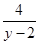，即y＝4时，等号成立，解得x＝6.
∴存在M，N点，当AM＝6，AN＝4时，Smin＝24.
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
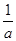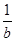－1)(
－1)(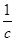
－1)≥8.
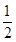，2)，其横截距与纵截距分别为a、b(a、b均为正数)，则使a＋b≥c恒成立的c的取值范围为________．
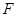（单位时间内测量点的车辆数，单位：辆/小时)与车流速度
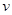（假设车辆以相同速度
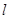（单位：米）的值有关，其公式为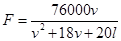
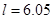，则最大车流量为_______辆/小时；
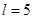，则最大车流量比（1）中的最大车流量增加 辆/小时.
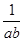的最小值为( )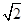
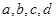满足：
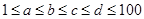,则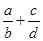
取得最小值时，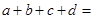
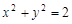的切线l与两坐标轴分别交于点A，B两点，则
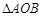（O为坐标原点）面积的最小值为 ．
，且
，若
，则必有
