题目内容
关于x的不等式组
的整数解的集合为A.
(1)当k=3时,求集合A;
(2)若集合A={-2},求实数k的取值范围;
(3)若集合A中有2013个元素,求实数k的取值范围.
|
(1)当k=3时,求集合A;
(2)若集合A={-2},求实数k的取值范围;
(3)若集合A中有2013个元素,求实数k的取值范围.
(1)当k=3时,由于第二个不等式的解为-3<x<-
,故满足条件的整数x不存在,故A=∅.
(2)由x2-x-2>0可得x<-1或x>2.
∵不等式组
的整数解为x=2,
又∵方程2x2+(2k+5)x+5k=0的两根为-k和-
.
①若-k<-
,则不等式组的整数解集合就不可能为{-2};
②若-
<-k,则应有-2<-k≤3.∴-3≤k<2.
综上,所求k的取值范围为[-3,2).
(3)当-k<-
时,A={-3,-4,…,-2015},所以-2016≤-k<-2015,得2015<k≤2016.
当-k>-
时,A={-2,3,…,2014},所以2014≤-k≤2015,得-2015≤k<-2014.
所以实数k的取值范围为(2015,2016],或[-2015,-2014).
| 5 |
| 2 |
(2)由x2-x-2>0可得x<-1或x>2.
∵不等式组
|
又∵方程2x2+(2k+5)x+5k=0的两根为-k和-
| 5 |
| 2 |
①若-k<-
| 5 |
| 2 |
②若-
| 5 |
| 2 |
综上,所求k的取值范围为[-3,2).
(3)当-k<-
| 5 |
| 2 |
当-k>-
| 5 |
| 2 |
所以实数k的取值范围为(2015,2016],或[-2015,-2014).

练习册系列答案
相关题目
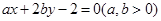 始终平分圆
始终平分圆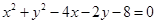 的周长,则
的周长,则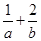 的最小值为 ( )
的最小值为 ( )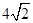
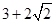
 的解集
的解集