题目内容
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 过点
过点![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右焦点,离心率为
的左、右焦点,离心率为![]() ,圆
,圆![]() 的直径为
的直径为![]() .
.
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() .
.
①若直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,求点
有且只有一个公共点,求点![]() 的坐标;
的坐标;
②若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)椭圆![]() :
:![]() ;圆
;圆![]() :
:![]() (2)①
(2)①![]() ,②
,②![]()
【解析】
(1)根据椭圆所过定点及离心率,结合椭圆中![]() 的关系,即可求得椭圆的标准方程;求得圆
的关系,即可求得椭圆的标准方程;求得圆![]() 的圆心和半径,即可得圆
的圆心和半径,即可得圆![]() 的方程.
的方程.
(2)①根据椭圆与圆的位置关系,可知当直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() ,且直线
,且直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点时,直线
有且只有一个公共点时,直线![]() 的斜率必小于0.设出直线方程
的斜率必小于0.设出直线方程![]() ,由直线与圆相切及点到直线距离公式,可得
,由直线与圆相切及点到直线距离公式,可得![]() 与
与![]() 的等量关系.联立直线方程与椭圆方程,由一个交点时
的等量关系.联立直线方程与椭圆方程,由一个交点时![]() 可得
可得![]() 与
与![]() 的等量关系.建立方程组可得
的等量关系.建立方程组可得![]() 与
与![]() 的值,即可求得直线方程.将直线方程与圆的方程联立,即可求得切点坐标.
的值,即可求得直线方程.将直线方程与圆的方程联立,即可求得切点坐标.
②设![]() ,将直线方程与椭圆方程联立,可得
,将直线方程与椭圆方程联立,可得![]() ,
,![]() ,由两个交点时
,由两个交点时![]() 可求得
可求得![]() 的取值范围.利用弦长公式
的取值范围.利用弦长公式![]() 表示出
表示出![]() ,由点到直线距离公式表示出
,由点到直线距离公式表示出![]() 到直线
到直线![]() 的距离
的距离![]() .结合
.结合![]() 的面积为
的面积为![]() 即可得
即可得![]() 与
与![]() 的等量关系.解方程求得
的等量关系.解方程求得![]() 与
与![]() 的值,即可求得直线方程.
的值,即可求得直线方程.
(1)椭圆![]() :
:![]() 过点
过点![]() ,离心率
,离心率![]()
所以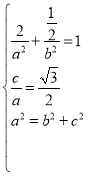 ,解方程组可得
,解方程组可得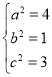
故椭圆![]() 的方程为
的方程为![]()
圆![]() 的直径为
的直径为![]() ,则圆心为
,则圆心为![]() ,半径为
,半径为![]()
所以圆![]() 的方程为
的方程为![]()
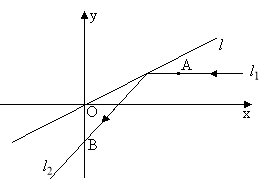
(2)①椭圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,如下图所示:
,如下图所示:
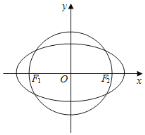
直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() ,且直线
,且直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,
有且只有一个公共点,
所以直线![]() 与椭圆
与椭圆![]() 也相切,且切点在第一象限,切点的纵坐标小于点
也相切,且切点在第一象限,切点的纵坐标小于点![]() 的纵坐标
的纵坐标
因而直线![]() 的斜率小于0
的斜率小于0
设直线![]() 的方程为
的方程为![]() ,即
,即![]()
因为直线![]() 与圆
与圆![]() 相切,则圆心到直线
相切,则圆心到直线![]() 的距离为圆的半径,即
的距离为圆的半径,即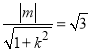 ,
,
化简可得![]()
因为直线![]() 与椭圆
与椭圆![]() 也相切,则
也相切,则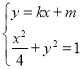
化简可得![]()
则![]()
解得![]()
所以![]()
解得![]() ,
,![]() (舍)
(舍)
则![]()
所以直线![]() 的方程为
的方程为![]()
则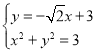 ,化简可得
,化简可得![]()
解得![]()
所以切点![]() 的坐标为
的坐标为![]()
②直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]()
联立直线![]() 与椭圆
与椭圆![]() ,则
,则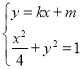
化简可得![]()
则![]()
![]()
由题意可知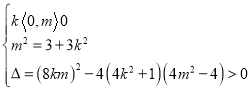
化简解不等式可得![]()
由弦长公式可得![]()
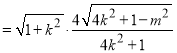
由点到直线距离公式可知![]() 到直线
到直线![]() 的距离
的距离![]()
则![]()
将![]() ,即
,即![]() 代入可解得
代入可解得![]()
即![]() ,
,![]() (舍),则
(舍),则![]()
所以直线![]() 的方程为
的方程为![]()

【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]()
【题目】英国统计学家E.H.辛普森1951年提出了著名的辛普森悖论,下面这个案例可以让我们感受到这个悖论.有甲乙两名法官,他们都在民事庭和行政庭主持审理案件,他们审理的部分案件被提出上诉.记录这些被上述案件的终审结果如下表所示(单位:件):
法官甲 | 法官乙 | ||||||
终审结果 | 民事庭 | 行政庭 | 合计 | 终审结果 | 民事庭 | 行政庭 | 合计 |
维持 | 29 | 100 | 129 | 维持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合计 | 32 | 118 | 150 | 合计 | 100 | 25 | 125 |
记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为
,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,则下面说法正确的是
,则下面说法正确的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()
【题目】![]() 是指悬浮在空气中的空气动力学当量直径小于或等于
是指悬浮在空气中的空气动力学当量直径小于或等于![]() 微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准
微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准![]() ,
,![]() 日均值在
日均值在![]() 微克/立方米以下,空气质量为一级;在
微克/立方米以下,空气质量为一级;在![]() 微克应立方米
微克应立方米![]() 微克立方米之间,空气质量为二级:在
微克立方米之间,空气质量为二级:在![]() 微克/立方米以上,空气质量为超标.从某市
微克/立方米以上,空气质量为超标.从某市![]() 年全年每天的
年全年每天的![]() 监测数据中随机地抽取
监测数据中随机地抽取![]() 天的数据作为样本,监测值频数如下表:
天的数据作为样本,监测值频数如下表:
(微克/立方米) |
|
|
|
|
|
|
频数(天) |
|
|
|
|
|
|
(1)从这![]() 天的
天的![]() 日均值监测数据中,随机抽出
日均值监测数据中,随机抽出![]() 天,求恰有
天,求恰有![]() 天空气质量达到一级的概率;
天空气质量达到一级的概率;
(2)从这![]() 天的数据中任取
天的数据中任取![]() 天数据,记
天数据,记![]() 表示抽到
表示抽到![]() 监测数据超标的天数,求
监测数据超标的天数,求![]() 的分布列.
的分布列.