题目内容
【题目】如图,等边三角形![]() 所在平面与梯形
所在平面与梯形![]() 所在平面互相垂直,且有
所在平面互相垂直,且有![]() ,
,![]() ,
,![]() .
.
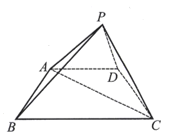
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由平面几何知识可得![]() ,再由面面垂直的性质定理得
,再由面面垂直的性质定理得![]() 平面
平面![]() ,最后由面面垂直的判定定理得结论;
,最后由面面垂直的判定定理得结论;
(2)取![]() 中点为
中点为![]() ,可得
,可得![]() ,从而有
,从而有![]() 平面
平面![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴建立空间直角坐标系(如图),写出各点坐标,求出平面
轴建立空间直角坐标系(如图),写出各点坐标,求出平面![]() 和平面
和平面![]() 的法向量,利用法向量的夹角得出二面角(注意二面角是锐角还是钝角).
的法向量,利用法向量的夹角得出二面角(注意二面角是锐角还是钝角).
(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,
,
则四边形![]() 为菱形,即有
为菱形,即有![]() ,
,
所以![]() .
.
又![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
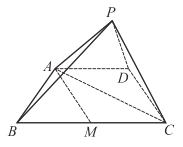
(2)由(1)可得![]() ,
,
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,![]() ,
,
又![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
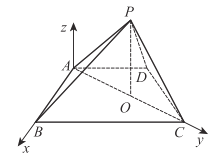
以![]() 为原点建系如图,则
为原点建系如图,则
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
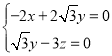 ,取
,取![]() ,得
,得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则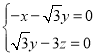 ,取
,取![]() ,
,![]() ,
,
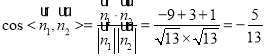 .
.
∴二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某集团公司为了加强企业管理,树立企业形象,考虑在公司内部对迟到现象进行处罚.现在员工中随机抽取200人进行调查,当不处罚时,有80人会迟到,处罚时,得到如下数据:
处罚金额 | 50 | 100 | 150 | 200 |
迟到的人数 | 50 | 40 | 20 | 0 |
若用表中数据所得频率代替概率.
(Ⅰ)当处罚金定为100元时,员工迟到的概率会比不进行处罚时降低多少?
(Ⅱ)将选取的200人中会迟到的员工分为![]() ,
,![]() 两类:
两类:![]() 类员工在罚金不超过100元时就会改正行为;
类员工在罚金不超过100元时就会改正行为;![]() 类是其他员工.现对
类是其他员工.现对![]() 类与
类与![]() 类员工按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为
类员工按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为![]() 类员工的概率是多少?
类员工的概率是多少?