题目内容
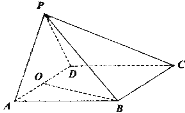
【题目】已知矩形
，
，
，将
沿对角线
进行翻折，得到三棱锥
，则在翻折的过程中，有下列结论正确的有_____.
①三棱锥的体积的最大值为
；
②三棱锥的外接球体积不变；
③三棱锥的体积最大值时，二面角
的大小是60°；
④异面直线
与
所成角的最大值为90°.
【答案】②④
【解析】
直接利用翻折问题的应用和面面垂直的应用和体积公式的应用和异面直线的夹角的应用求出结果.
解：矩形
，
，将
沿对角线
进行翻折，得到三棱锥
，则在翻折的过程中，
①
，当平面
平面
时，三棱锥的高最大，此时三棱锥的体积
，
所以三棱锥的体积的最大值为
，故错误；
②设的中点为O，则由
，
知：
，
所以O为三棱锥外接球的球心，其半径为
，
所以外接球的体积为
，三棱锥的外接球体积不变，故正确.
③三棱锥的体积最大值时，当平面平面时，二面角
的大小是90°，故错误.
④当
沿对角线进行翻折到使点D与点B的距离为
，即
时，在
中，
，所以
，又
，
翻折后的垂直关系没有变，所以
平面
，即异面直线
与
所成角的最大值为90°，故正确.
故答案为：②④.
练习册系列答案
相关题目
