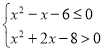题目内容
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,
,![]() ,
,![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(Ⅰ)求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
试题(1)由题意知,![]() 的可能取值为
的可能取值为![]() ,
,![]() ,
,![]() ,
,![]() ,分别求出相应的概率,由此能求出
,分别求出相应的概率,由此能求出![]() 的分布列和
的分布列和![]() ;(2)由
;(2)由![]() 表示“甲队得分等于
表示“甲队得分等于![]() 乙队得分等于
乙队得分等于![]() ”,
”,![]() 表示“甲队得分等于
表示“甲队得分等于![]() 乙队得分等于
乙队得分等于![]() ”,可知
”,可知![]() 、
、![]() 互斥.利用互斥事件的概率计算公式即可得出甲、乙两队总得分之和等于
互斥.利用互斥事件的概率计算公式即可得出甲、乙两队总得分之和等于![]() 分且甲队获胜的概率.
分且甲队获胜的概率.
试题解析:(1)由题意知,![]() 的所有可能取值为
的所有可能取值为![]() .
.![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
![]() .
.
(2)用![]() 表示“甲得
表示“甲得![]() 分乙得
分乙得![]() 分”, 用
分”, 用![]() 表示“甲得
表示“甲得![]() 分乙得
分乙得![]() 分”, 且
分”, 且![]() 互斥,
互斥,
又![]() ,
,![]() ,甲、乙两队得分总和为
,甲、乙两队得分总和为![]() 分且甲获胜的概率为
分且甲获胜的概率为![]() .
.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
【题目】某汽车公司为调查4S店个数对该公司汽车销量的影响,对同等规模的A,B,C,D四座城市的4S店一个月某型号汽车销量进行了统计,结果如下表:
城市 | A | B | C | D |
4S店个数x | 3 | 4 | 6 | 7 |
销售台数y | 18 | 26 | 34 | 42 |
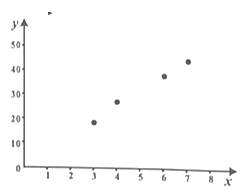
(1)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程;
(2)根据统计每个城市汽车的盈利![]() (万元)与该城市4S店的个数x符合函数
(万元)与该城市4S店的个数x符合函数![]() ,
,![]() ,为扩大销售,该公司在同等规模的城市E预计要开设多少个4S店,才能使E市的4S店一个月某型号骑车销售盈利达到最大,并求出最大值.
,为扩大销售,该公司在同等规模的城市E预计要开设多少个4S店,才能使E市的4S店一个月某型号骑车销售盈利达到最大,并求出最大值.
附:回归方程![]() 中的斜率和截距的最小二乘法估计公式分别为:
中的斜率和截距的最小二乘法估计公式分别为: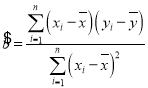 ,
,![]()