题目内容
【题目】如图,菱形![]() 与正三角形
与正三角形![]() 的边长均为2,它们所在平面互相垂直,
的边长均为2,它们所在平面互相垂直,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)见证明;(2) ![]()
【解析】
(1)由菱形的性质可得![]() ,由线面垂直的性质可得
,由线面垂直的性质可得![]() ,从而可得
,从而可得![]() 平面
平面![]() ,再由面面垂直的判定定理可得结果;(2)设
,再由面面垂直的判定定理可得结果;(2)设![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,利用向量垂直数量积为零列方程求得平面
轴,建立空间直角坐标系,利用向量垂直数量积为零列方程求得平面![]() 的法向量,结合平面
的法向量,结合平面![]() 的法向量
的法向量![]() ,利用空间向量夹角余弦公式可得结果.
,利用空间向量夹角余弦公式可得结果.
(1)∵菱形![]() ,∴
,∴![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)设![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,
过![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
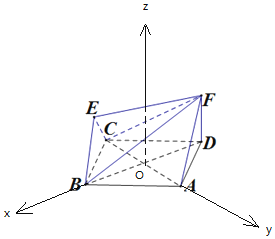
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则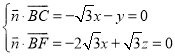 ,取
,取![]() ,得
,得![]() ,
,
平面![]() 的法向量
的法向量![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,
,
则![]() ,
,
∴![]() .
.
∴二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
【题目】在新的劳动合同法出台后,某公司实行了年薪制工资结构改革.该公司从2008年起,每人的工资由三个项目构成,并按下表规定实施:
项目 | 金额[元/(人年)] | 性质与计算方法 |
基础工资 | 2007年基础工资为20000元 | 考虑到物价因素,决定从2008年 起每年递增10%(与工龄无关) |
房屋补贴 | 800 | 按职工到公司年限计算,每年递增800元 |
医疗费 | 3200 | 固定不变 |
如果该公司今年有5位职工,计划从明年起每年新招5名职工.
(1)若今年算第一年,将第n年该公司付给职工工资总额y(万元)表示成年限n的函数;
(2)若公司每年发给职工工资总额中,房屋补贴和医疗费的总和总不会超过基础工资总额的p%,求p的最小值.