题目内容
【题目】已知a,b为异面直线,且所成的角为70°,过空间一点作直线l,直线l与a,b均异面,且所成的角均为50°,则满足条件的直线共有( ) 条
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
在空间取一过点P的平面α,过点P分别作a,b的平行线a′、b′,则a′、b′所成锐角等于70°,所成钝角为110°,当过P的直线PM的射影P在a′、b′所成锐角或钝角的平分线上时,PM与两条直线a,b所成的角相等,分别求出两种情况下PM与a,b的夹角的范围,根据对称性即可得出答案.
在空间取一点P,经过点P分别作a∥a′,b∥b′,
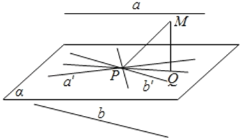
设直线a′、b′确定平面α,
当直线PM满足它的射影PQ在a′、b′所成角的平分线上时,
PM与a′所成的角等于PM与b′所成的角.
因为直线a,b所成的角为70°,得a′、b′所成锐角等于70°.
所以当PM的射影PQ在a′、b′所成锐角的平分线上时,
PM与a′、b′所成角的范围是[35°,90°).
这种情况下,过点P有两条直线与a′、b′所成的角都是50°.
当PM的射影PQ在a′、b′所成钝角的平分线上时,PM与a′、b′所成角的范围是[55°,90°).
这种情况下,过点P有0条直线(即PMα时)与a′、b′所成的角都是50°.
综上所述,过空间任意一点P可作与a,b所成的角都是50°的直线有2条.
故选:B.

【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下: 
(Ⅰ)记A表示时间“旧养殖法的箱产量低于50kg”,估计A的概率;
(Ⅱ)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(Ⅲ)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.
附:
P(K2≥K) | 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
K2= ![]() .
.