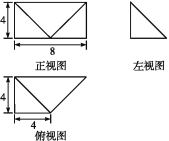
题目内容
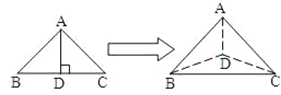
【题目】如图，在Rt△ABC中，AB＝BC＝4，点E在线段AB上．过点E作EF∥BC交AC于点F，将△AEF沿EF折起到△PEF的位置(点A与P重合)，使得∠PEB＝60°.
(1)求证：EF⊥PB.
(2)试问：当点E在线段AB上移动时，二面角PFCB的平面角的余弦值是否为定值？若是，求出其定值；若不是，说明理由．
【答案】⑴见证明；⑵当点E在线段AB上移动时，二面角PFCB的平面角的余弦值为定值，且定值为
.
【解析】
（1）由已知在Rt△ABC中，中EF∥BC，我们可得到EF⊥AB，即EF⊥EB，EF⊥EP，由线面垂直的判定定理定理，易得EF⊥平面PEB，再由线面垂直的定义，即可得到EF丄PB；
（2）在平面PEB中，过P点作PD⊥BE于D，结合（I）的结论可得BH⊥平面BCFE，以B为坐标原点，BC，BE，BH方向分别为X，Y，Z轴正方向建立空间坐标系，则我们可以分别求出平面PFC与平面BFC的法向量，代入二面角的向量夹角公式中，求出其余弦值，判断后，即可得到答案．
（1）证明：在Rt△ABC中，∵EF∥BC
∴EF⊥AB
∴EF⊥EB，EF⊥EP，又由EB∩EP=E
∴EF⊥平面PEB
又∵PB平面PEB
∴EF⊥PB
（2）在平面PEB中，过P点作PD⊥BE于D，
由（1）知，EF⊥PD
∴PD⊥平面BCFE
在平面PEB中过点B作直线BH∥PD
则BH⊥平面BCFE
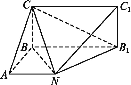
如图，以B为坐标原点，BC，BE，BH方向分别为X，Y，Z轴正方向建立空间坐标系，
设PE=x（0＜x＜4），又∵AB=BC=4
∴BE=4﹣x，EF=x
在Rt△PED中，∠PED=60°
∴PD=
，DE=
∴BD=4﹣x﹣=4﹣
∴C（4，0，0），F（x，4﹣x，0），P（0，4﹣，）
从而
=（x﹣4，4﹣x，0），
=（﹣4，4﹣，）
设
=（a，b，c）是平面PCF的一个法向量，则：
，
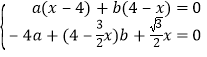即
令b=1，则=（1，1，
）是平面PCF的一个法向量，
又∵平面BCF的一个法向量为
=（0，0，1）
设二面角P﹣FC﹣B的平面角为θ，则
Cosθ=
=
∴当点E在线段AB上移动时，二面角P﹣FC﹣B的平面角的余弦值为定值
