题目内容
【题目】（本小题满分14分）
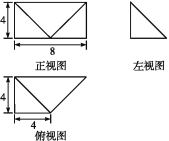
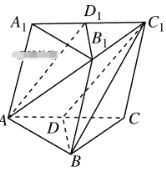
如图1，在三棱锥P－ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上一点，它的正(主)视图和侧(左)视图如图2所示．
(1) 证明：AD⊥平面PBC；
(2) 在∠ACB的平分线上确定一点Q，使得PQ∥平面ABD，并求此时PQ的长．
【答案】（1）详见解析；（2）
.
【解析】
(1)易证
再证
即可.
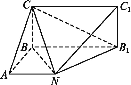
(II) 确定Q的位置是解决此问题的关键：取AB的中点O，连接CO并延长至Q，使得CQ＝2CO，连接PQ，OD，点Q即为所求．
证明：（1）因为
，
，所以
又因为
，所以
，所以
………………4分
由三视图可得在
中，
，
为
的中点，所以
所以
………………………………………6分
(2)取AB的中点O，连接CO并延长至Q，使得CQ＝2CO，
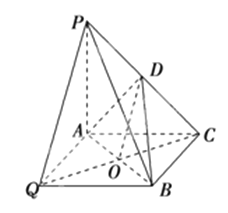
连接PQ，OD，点Q即为所求．………………8分
因为O为CQ的中点，D为PC的中点，所以
…………………………10分
连接AQ,BQ,
四边形
的对角线互相平分，且
,
四边形为正方形，
即为
的平分线
又
，
在直角三角形
中，
………………14分
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
【题目】已知一个口袋有m个白球，n个黑球（m，n∈N* ， n≥2），这些球除颜色外全部相同．现将口袋中的球随机的逐个取出，并放入如图所示的编号为1，2，3，…，m+n的抽屉内，其中第k次取出的球放入编号为k的抽屉（k=1，2，3，…，m+n）．
1 | 2 | 3 | … | m+n |
（Ⅰ）试求编号为2的抽屉内放的是黑球的概率p；
（Ⅱ）随机变量x表示最后一个取出的黑球所在抽屉编号的倒数，E（X）是X的数学期望，证明E（X）＜ 
．
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg），其频率分布直方图如下： 
（Ⅰ）记A表示时间“旧养殖法的箱产量低于50kg”，估计A的概率；
（Ⅱ）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：
箱产量＜50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
（Ⅲ）根据箱产量的频率分布直方图，对两种养殖方法的优劣进行比较．
附：
P（K2≥K） | 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
K2= 
．
