题目内容
已知数列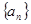 满足:
满足: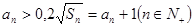 ,其中
,其中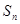 为
为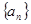 的前
的前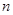 项和。
项和。
(1)求数列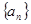 的通项公式;
的通项公式;
(2)若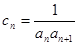 ,
,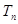 为
为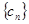 的前
的前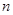 项和,且对任意
项和,且对任意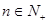 ,不等式
,不等式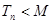 恒成立,求整数
恒成立,求整数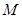 的最小值。
的最小值。
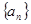 满足:
满足: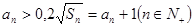 ,其中
,其中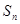 为
为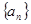 的前
的前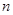 项和。
项和。(1)求数列
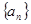 的通项公式;
的通项公式;(2)若
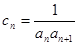 ,
,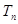 为
为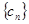 的前
的前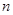 项和,且对任意
项和,且对任意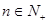 ,不等式
,不等式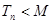 恒成立,求整数
恒成立,求整数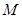 的最小值。
的最小值。(1)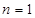 时,
时,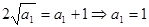 ,由
,由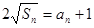 ,得
,得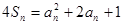 ,
,
所以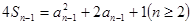 ,两式相减得:
,两式相减得: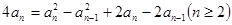 ,
,
化简得: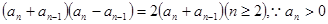 ,所以
,所以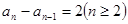 ,
,
所以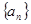 为等差数列,通项公式是
为等差数列,通项公式是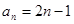 ;
;
(2)由(1)知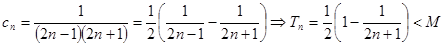 恒成立,则
恒成立,则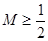 ,由
,由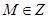 ,所以
,所以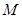 的最小值是1。
的最小值是1。
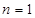 时,
时,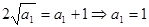 ,由
,由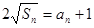 ,得
,得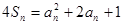 ,
,所以
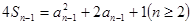 ,两式相减得:
,两式相减得: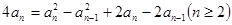 ,
,化简得:
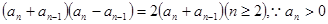 ,所以
,所以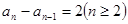 ,
,所以
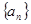 为等差数列,通项公式是
为等差数列,通项公式是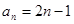 ;
;(2)由(1)知
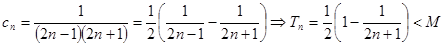 恒成立,则
恒成立,则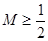 ,由
,由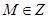 ,所以
,所以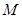 的最小值是1。
的最小值是1。略

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
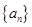 中,
中,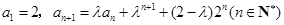 ,其中
,其中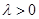 .
.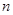 项和
项和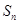 ;
;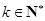 ,使得
,使得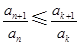 对任意
对任意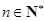 均成立.
均成立.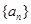 的前n项和为
的前n项和为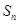 ,令
,令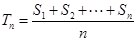 ,称
,称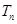 为数列
为数列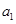 ,
,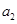 ,……,
,……,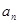 的“和平均数”,已知数列
的“和平均数”,已知数列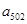 的“和平均数”为2012,那么数列2,
的“和平均数”为2012,那么数列2,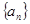 的前
的前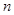 项和
项和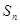 满足:
满足: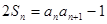 ,
,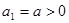
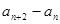 是一个定值;
是一个定值;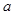 的取值范围;
的取值范围;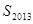 是一个整数,求符合条件的自然数
是一个整数,求符合条件的自然数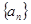 的前
的前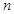 项和,
项和,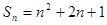 。
。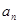 ;
;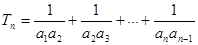 ,求
,求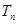 .
.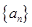 满足:
满足: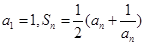 ,其中
,其中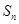 为其前
为其前 项和,则
项和,则 ____
____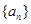 的首项为
的首项为 ,公差为b,等比数列
,公差为b,等比数列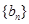 的首项为b,公比为a(其中a,b均为正整数)。
的首项为b,公比为a(其中a,b均为正整数)。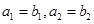 ,求数列
,求数列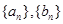 的通项公式;
的通项公式; ,对任意
,对任意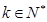 在
在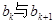 之间插入
之间插入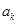 个2,得到一个新的数列
个2,得到一个新的数列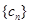 ,试求满足等式
,试求满足等式 的所有正整数m的值;
的所有正整数m的值;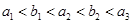 ,若存在正整数m,n以及至少三个不同的b值使得等
,若存在正整数m,n以及至少三个不同的b值使得等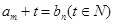 成立,求t的最小值,并求t最小时a,b的值。
成立,求t的最小值,并求t最小时a,b的值。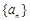 中,
中,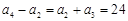 .记数列
.记数列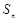 .
.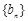 中,
中,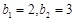 ,数列
,数列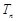 满足:
满足: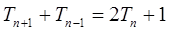 ,
,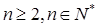 , 求:
, 求: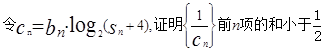 .
.