题目内容
(本题满分共14分)已知数列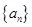 ,
,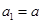 ,且
,且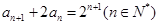 ,
,
(1)若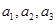 成等差数列,求实数
成等差数列,求实数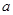 的值;(2)数列
的值;(2)数列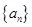 能为等比数列吗?若能,
能为等比数列吗?若能,
试写出它的充要条件并加以证明;若不能,请说明理由。
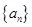 ,
,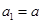 ,且
,且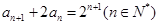 ,
,(1)若
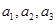 成等差数列,求实数
成等差数列,求实数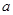 的值;(2)数列
的值;(2)数列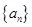 能为等比数列吗?若能,
能为等比数列吗?若能,试写出它的充要条件并加以证明;若不能,请说明理由。
解.(Ⅰ)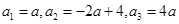 ,
,
因为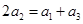 ,所以
,所以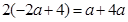 ,得
,得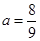
(Ⅱ)方法一:因为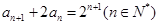 ,所以
,所以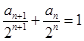 ,
,
得: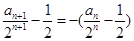 ,故
,故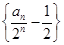 是以
是以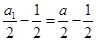 为首项,
为首项,
-1为公比的等比数列,
所以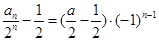 ,得:
,得: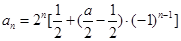
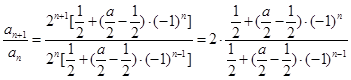
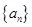 为等比数列
为等比数列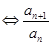 为常数,易得当且仅当
为常数,易得当且仅当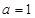 时,
时,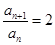 为常数。
为常数。
方法二:因为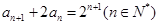 ,所以
,所以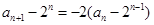 ,
,
即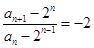 ,故
,故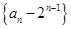 是以
是以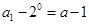 为首项,-2为公比的成等比数列,
为首项,-2为公比的成等比数列,
所以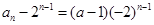 ,得:
,得: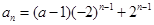 (下同解法一)
(下同解法一)
方法三:由前三项成等比得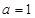 ,进而猜测
,进而猜测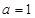 ,对于所有情况都成立,再证明。
,对于所有情况都成立,再证明。
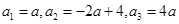 ,
,因为
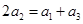 ,所以
,所以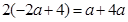 ,得
,得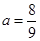
(Ⅱ)方法一:因为
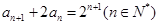 ,所以
,所以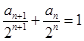 ,
,得:
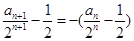 ,故
,故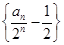 是以
是以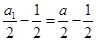 为首项,
为首项,-1为公比的等比数列,
所以
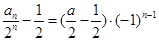 ,得:
,得: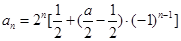
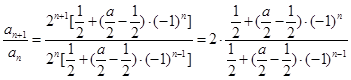
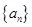 为等比数列
为等比数列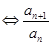 为常数,易得当且仅当
为常数,易得当且仅当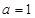 时,
时,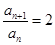 为常数。
为常数。方法二:因为
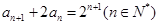 ,所以
,所以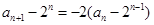 ,
,即
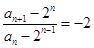 ,故
,故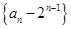 是以
是以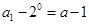 为首项,-2为公比的成等比数列,
为首项,-2为公比的成等比数列,所以
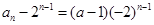 ,得:
,得: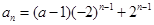 (下同解法一)
(下同解法一)方法三:由前三项成等比得
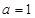 ,进而猜测
,进而猜测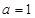 ,对于所有情况都成立,再证明。
,对于所有情况都成立,再证明。略

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
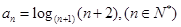 ,我们把使乘积
,我们把使乘积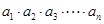 为整数的数
为整数的数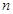 叫做“劣数”,则在区间
叫做“劣数”,则在区间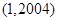 内的所有劣数的和为
内的所有劣数的和为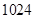
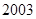
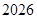
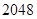
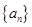 中,
中,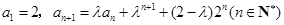 ,其中
,其中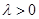 .
.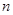 项和
项和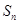 ;
;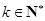 ,使得
,使得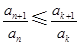 对任意
对任意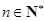 均成立.
均成立.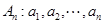 .如果数列
.如果数列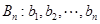 满足
满足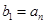 ,
,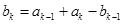 ,其中
,其中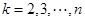 ,则称
,则称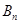 为
为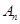 的“衍生数列”.
的“衍生数列”.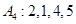 的“衍生数列”
的“衍生数列”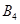 ;
;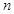 为偶数,且
为偶数,且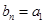 ;
;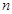 为奇数,且
为奇数,且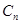 ,….依次将数
,….依次将数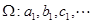 .证明:
.证明: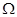 是等差数列.
是等差数列.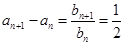 (n="1," 2, 3,……),cn=anbn, 试求
(n="1," 2, 3,……),cn=anbn, 试求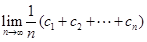 (12分)
(12分)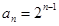 , 则
, 则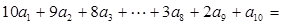 ▲ .
▲ . 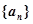 ,
,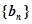 满足
满足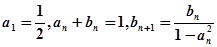
 ,则
,则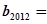 ▲ .
▲ .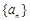 中,
中,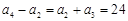 .记数列
.记数列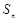 .
.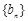 中,
中,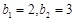 ,数列
,数列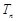 满足:
满足: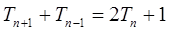 ,
,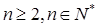 , 求:
, 求: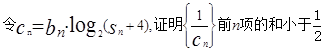 .
. 其一半,图(3)用图(2)的方法在每一线段前端生成两条线段,长度为其一半,重复前面的作法至第n张图,设第n个图形所有线段长之和为an,第n个图形,最短的线段长之和为bn,设
其一半,图(3)用图(2)的方法在每一线段前端生成两条线段,长度为其一半,重复前面的作法至第n张图,设第n个图形所有线段长之和为an,第n个图形,最短的线段长之和为bn,设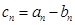 ,则cn=
,则cn=