题目内容
(本小题满分14分)
一个几何体是由圆柱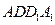 和三棱锥
和三棱锥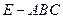 组合而成,点
组合而成,点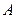 、
、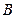 、
、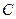 在圆
在圆 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中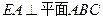 ,
,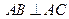 ,
,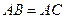 ,
,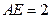 .
.
(1)求证: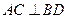 ;
;
(2)求二面角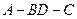 的平面角的大小.
的平面角的大小.

一个几何体是由圆柱
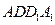 和三棱锥
和三棱锥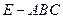 组合而成,点
组合而成,点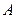 、
、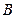 、
、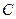 在圆
在圆 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中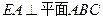 ,
,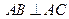 ,
,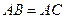 ,
,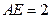 .
.(1)求证:
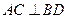 ;
;(2)求二面角
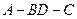 的平面角的大小.
的平面角的大小.
(本小题主要考查空间线线、线面关系,二面角,三视图等知识,考查化归与转化数学思想方法,以及空间想象能力、推理论证能力、运算求解能力.)
方法1:(1)证明:因为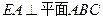 ,
,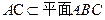 ,所以
,所以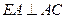 ,即
,即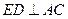 .
.
又因为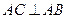 ,
,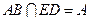 ,所以
,所以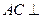 平面
平面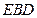 .
.
因为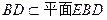 ,所以
,所以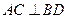 .………………………………………………………………4分
.………………………………………………………………4分
(2)解:因为点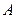 、
、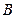 、
、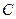 在圆
在圆 的圆周上,且
的圆周上,且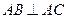 ,所以
,所以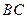 为圆
为圆 的直径.
的直径.
设圆 的半径为
的半径为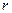 ,圆柱高为
,圆柱高为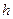 ,根据正(主)视图、侧(左)视图的面积可得,
,根据正(主)视图、侧(左)视图的面积可得,
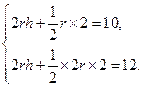 …………………………………………6分
…………………………………………6分
解得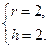
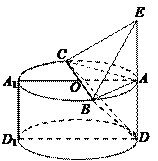
所以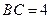 ,
,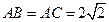 .………………………………………………………………………7分
.………………………………………………………………………7分
过点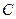 作
作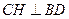 于点
于点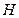 ,连接
,连接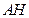 ,
,
由(1)知,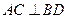 ,
,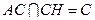 ,所以
,所以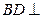 平面
平面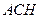 .
.
因为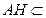 平面
平面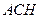 ,所以
,所以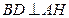 .
.
所以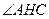 为二面角
为二面角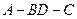 的平面角.…………………………………………………………9分
的平面角.…………………………………………………………9分
由(1)知,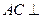 平面
平面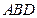 ,
,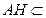 平面
平面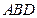 ,
,
所以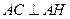 ,即△
,即△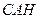 为直角三角形.
为直角三角形.
在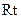 △
△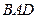 中,
中,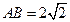 ,
,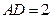 ,则
,则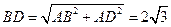 .
.
由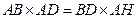 ,解得
,解得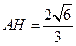 .
.
因为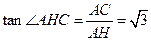 .…………………………………………………………………………13分
.…………………………………………………………………………13分
所以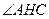
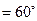 .
.
所以二面角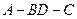 的平面角大小为
的平面角大小为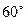 .………………………………………………………14分
.………………………………………………………14分
方法2:(1)证明:因为点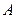 、
、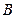 、
、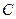 在圆
在圆 的圆周上,且
的圆周上,且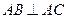 ,所以
,所以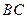 为圆
为圆 的直径.
的直径.
设圆 的半径为
的半径为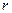 ,圆柱高为
,圆柱高为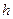 ,根据正(主)视图、侧(左)视图的面积可得,
,根据正(主)视图、侧(左)视图的面积可得,
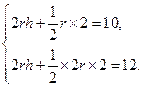 …………………………………………2分
…………………………………………2分
解得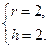
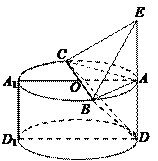
所以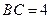 ,
,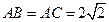 .………………………………………………………………………3分
.………………………………………………………………………3分
以点 为原点,
为原点,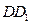 、
、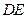 所在的射线分别为
所在的射线分别为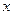 轴、
轴、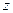 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系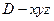 ,则
,则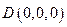 ,
,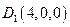 ,
,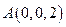 ,
,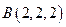 ,
,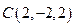 ,
,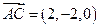 ,
,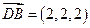 .
.
………………………5分
因为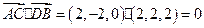 ,
,
所以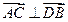 .
.
所以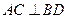 .…………………………………………………9分
.…………………………………………………9分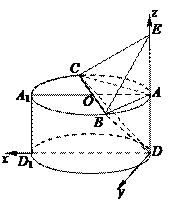
(2)解:设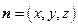 是平面
是平面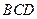 的法向量,因为
的法向量,因为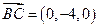 ,
,
所以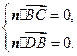 即
即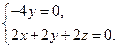
取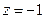 ,则
,则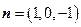 是平面
是平面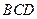 的一个法向量.……………………………………………11分
的一个法向量.……………………………………………11分
由(1)知,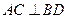 ,又
,又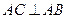 ,
,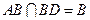 ,所以
,所以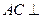 平面
平面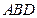 .
.
所以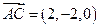 是平面
是平面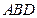 的一个法向量.……………………………………………………12分
的一个法向量.……………………………………………………12分
因为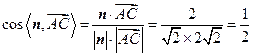 ,
,
所以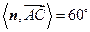 .
.
而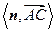 等于二面角
等于二面角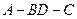 的平面角,
的平面角,
所以二面角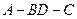 的平面角大小为
的平面角大小为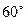 .………………………………………………………14分
.………………………………………………………14分
方法3:(1)证明:因为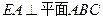 ,
,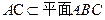 ,所以
,所以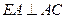 ,即
,即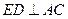 .
.
又因为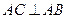 ,
,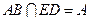 ,所以
,所以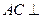 平面
平面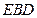 .
.
因为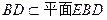 ,
,
所以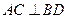 .…………………………………………………………………………………………4分
.…………………………………………………………………………………………4分
(2)解:因为点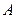 、
、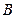 、
、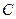 在圆
在圆 的圆周上,且
的圆周上,且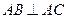 ,所以
,所以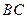 为圆
为圆 的直径.
的直径.
设圆 的半径为
的半径为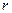 ,圆柱高为
,圆柱高为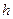 ,根据正(主)视图、侧(左)视图的面积可得,
,根据正(主)视图、侧(左)视图的面积可得,
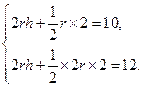 …………………………………………6分
…………………………………………6分
解得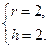
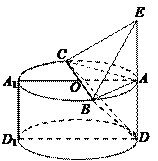
所以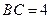 ,
,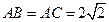 .………………………………………………………………………7分
.………………………………………………………………………7分
以点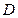 为原点,
为原点,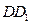 、
、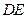 所在的射线分别为
所在的射线分别为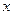 轴、
轴、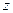 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系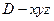 ,则
,则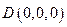 ,
,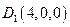 ,
,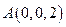 ,
,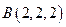 ,
,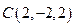 ,
,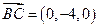 ,
,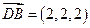 .
.
…………………………9分
设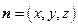 是平面
是平面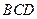 的法向量,
的法向量,
则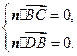 即
即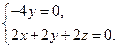
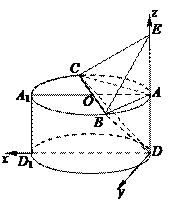
取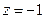 ,则
,则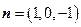 是平面
是平面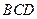 的一个法向量.………11分
的一个法向量.………11分
由(1)知,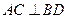 ,又
,又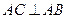 ,
,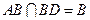 ,
,
所以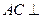 平面
平面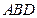 .
.
所以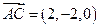 是平面
是平面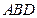 的一个法向量.……………………………………………………12分
的一个法向量.……………………………………………………12分
因为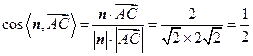 ,
,
所以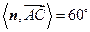 .
.
而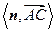 等于二面角
等于二面角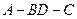 的平面角,
的平面角,
所以二面角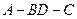 的平面角大小为
的平面角大小为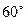 .………………………………………………………14分
.………………………………………………………14分
方法1:(1)证明:因为
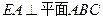 ,
,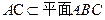 ,所以
,所以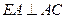 ,即
,即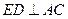 .
.又因为
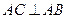 ,
,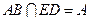 ,所以
,所以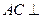 平面
平面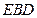 .
.因为
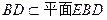 ,所以
,所以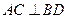 .………………………………………………………………4分
.………………………………………………………………4分(2)解:因为点
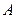 、
、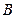 、
、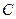 在圆
在圆 的圆周上,且
的圆周上,且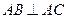 ,所以
,所以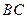 为圆
为圆 的直径.
的直径.设圆
 的半径为
的半径为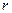 ,圆柱高为
,圆柱高为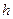 ,根据正(主)视图、侧(左)视图的面积可得,
,根据正(主)视图、侧(左)视图的面积可得,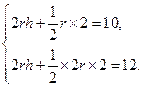 …………………………………………6分
…………………………………………6分解得
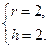
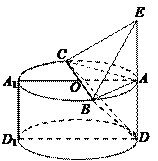
所以
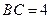 ,
,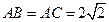 .………………………………………………………………………7分
.………………………………………………………………………7分过点
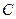 作
作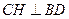 于点
于点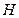 ,连接
,连接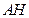 ,
,由(1)知,
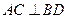 ,
,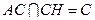 ,所以
,所以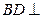 平面
平面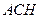 .
.因为
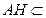 平面
平面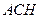 ,所以
,所以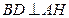 .
.所以
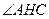 为二面角
为二面角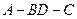 的平面角.…………………………………………………………9分
的平面角.…………………………………………………………9分由(1)知,
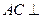 平面
平面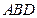 ,
,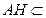 平面
平面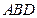 ,
,所以
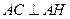 ,即△
,即△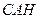 为直角三角形.
为直角三角形.在
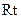 △
△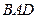 中,
中,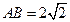 ,
,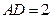 ,则
,则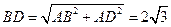 .
. 由
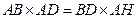 ,解得
,解得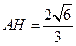 .
. 因为
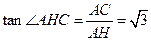 .…………………………………………………………………………13分
.…………………………………………………………………………13分所以
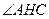
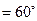 .
.所以二面角
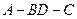 的平面角大小为
的平面角大小为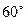 .………………………………………………………14分
.………………………………………………………14分方法2:(1)证明:因为点
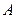 、
、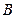 、
、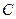 在圆
在圆 的圆周上,且
的圆周上,且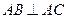 ,所以
,所以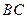 为圆
为圆 的直径.
的直径.设圆
 的半径为
的半径为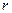 ,圆柱高为
,圆柱高为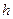 ,根据正(主)视图、侧(左)视图的面积可得,
,根据正(主)视图、侧(左)视图的面积可得,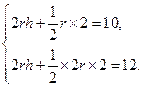 …………………………………………2分
…………………………………………2分解得
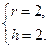
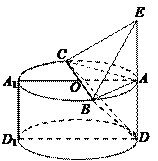
所以
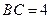 ,
,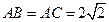 .………………………………………………………………………3分
.………………………………………………………………………3分以点
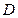 为原点,
为原点,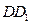 、
、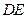 所在的射线分别为
所在的射线分别为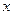 轴、
轴、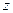 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系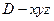 ,则
,则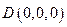 ,
,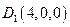 ,
,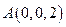 ,
,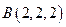 ,
,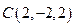 ,
,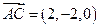 ,
,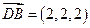 .
.………………………5分
因为
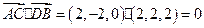 ,
,所以
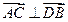 .
.所以
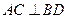 .…………………………………………………9分
.…………………………………………………9分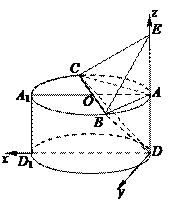
(2)解:设
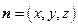 是平面
是平面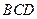 的法向量,因为
的法向量,因为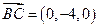 ,
,所以
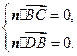 即
即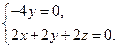
取
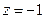 ,则
,则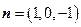 是平面
是平面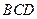 的一个法向量.……………………………………………11分
的一个法向量.……………………………………………11分由(1)知,
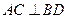 ,又
,又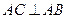 ,
,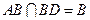 ,所以
,所以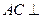 平面
平面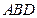 .
.所以
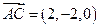 是平面
是平面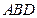 的一个法向量.……………………………………………………12分
的一个法向量.……………………………………………………12分因为
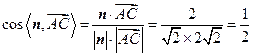 ,
,所以
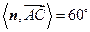 .
.而
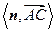 等于二面角
等于二面角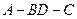 的平面角,
的平面角,所以二面角
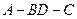 的平面角大小为
的平面角大小为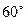 .………………………………………………………14分
.………………………………………………………14分方法3:(1)证明:因为
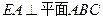 ,
,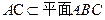 ,所以
,所以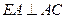 ,即
,即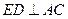 .
.又因为
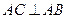 ,
,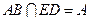 ,所以
,所以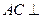 平面
平面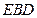 .
.因为
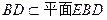 ,
,所以
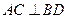 .…………………………………………………………………………………………4分
.…………………………………………………………………………………………4分(2)解:因为点
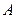 、
、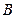 、
、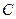 在圆
在圆 的圆周上,且
的圆周上,且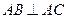 ,所以
,所以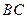 为圆
为圆 的直径.
的直径.设圆
 的半径为
的半径为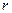 ,圆柱高为
,圆柱高为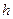 ,根据正(主)视图、侧(左)视图的面积可得,
,根据正(主)视图、侧(左)视图的面积可得,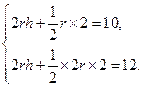 …………………………………………6分
…………………………………………6分解得
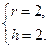
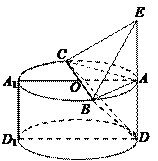
所以
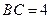 ,
,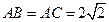 .………………………………………………………………………7分
.………………………………………………………………………7分以点
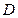 为原点,
为原点,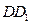 、
、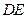 所在的射线分别为
所在的射线分别为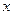 轴、
轴、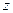 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系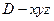 ,则
,则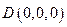 ,
,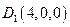 ,
,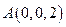 ,
,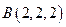 ,
,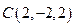 ,
,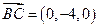 ,
,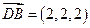 .
.…………………………9分
设
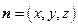 是平面
是平面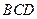 的法向量,
的法向量,则
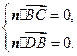 即
即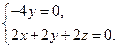
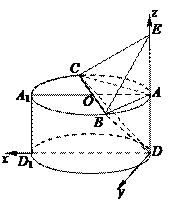
取
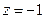 ,则
,则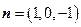 是平面
是平面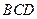 的一个法向量.………11分
的一个法向量.………11分由(1)知,
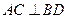 ,又
,又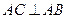 ,
,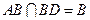 ,
,所以
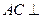 平面
平面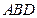 .
.所以
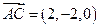 是平面
是平面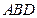 的一个法向量.……………………………………………………12分
的一个法向量.……………………………………………………12分因为
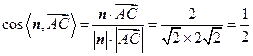 ,
,所以
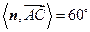 .
.而
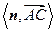 等于二面角
等于二面角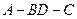 的平面角,
的平面角,所以二面角
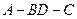 的平面角大小为
的平面角大小为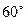 .………………………………………………………14分
.………………………………………………………14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
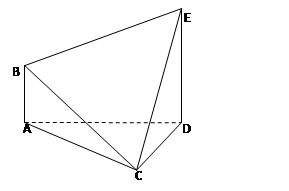
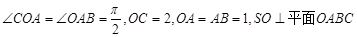 ,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.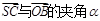 的余弦值;
的余弦值;
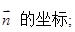
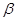 ,求
,求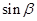 。
。
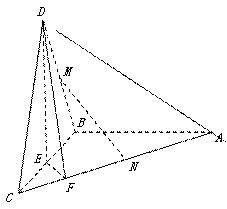
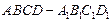 的棱长为
的棱长为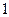 ,点
,点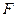 为
为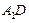 的中点.
的中点.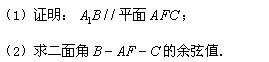
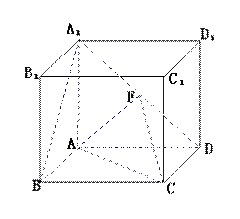
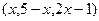 ,B
,B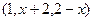 ,当
,当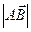 取最小值时,
取最小值时,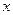 的值等于( )
的值等于( )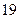
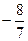
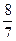
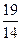
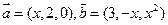 ,且
,且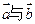 的夹角为钝角,则
的夹角为钝角,则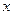 的取值范围是( )
的取值范围是( )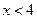
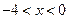
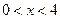
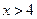
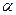 内有一点
内有一点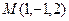 ,平面
,平面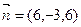 ,则下列点
,则下列点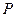 中,在平面
中,在平面