题目内容
与椭圆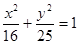 共焦点,且过点(-2,
共焦点,且过点(-2,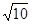 )的双曲线方程为( )
)的双曲线方程为( )
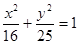 共焦点,且过点(-2,
共焦点,且过点(-2,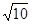 )的双曲线方程为( )
)的双曲线方程为( )A. | B.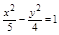 | C.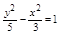 | D.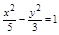 |
C
A
由椭圆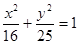 焦点为F(0,±3),设与椭圆
焦点为F(0,±3),设与椭圆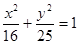 共焦点的双曲线设为
共焦点的双曲线设为 =1,再由双曲线过点(-2,
=1,再由双曲线过点(-2,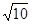 ),能求出双曲线方程.
),能求出双曲线方程.
解答:解:∵椭圆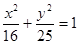 焦点为F(0,±3),
焦点为F(0,±3),
∴与椭圆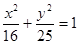 共焦点的双曲线设为
共焦点的双曲线设为
∵双曲线过点(-2,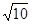 ),
),
∴ =1,
=1,
整理,得a4-23a2+90=0,
解得a2=5,或a2=18(舍).
∴双曲线方程为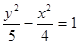 故选A.
故选A.
由椭圆
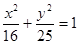 焦点为F(0,±3),设与椭圆
焦点为F(0,±3),设与椭圆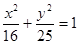 共焦点的双曲线设为
共焦点的双曲线设为 =1,再由双曲线过点(-2,
=1,再由双曲线过点(-2,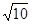 ),能求出双曲线方程.
),能求出双曲线方程.解答:解:∵椭圆
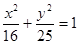 焦点为F(0,±3),
焦点为F(0,±3),∴与椭圆
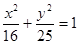 共焦点的双曲线设为
共焦点的双曲线设为
∵双曲线过点(-2,
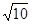 ),
),∴
 =1,
=1,整理,得a4-23a2+90=0,
解得a2=5,或a2=18(舍).
∴双曲线方程为
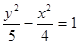 故选A.
故选A.
练习册系列答案
相关题目
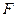 是椭圆
是椭圆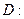
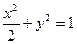 的右焦点,过点
的右焦点,过点 且斜率为
且斜率为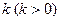 的直线
的直线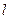 与
与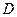 交于
交于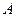 、
、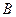 两点,
两点,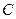 是点
是点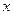 轴的对称点.
轴的对称点.
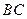 上;
上;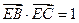 ,求
,求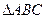 外接圆的方程.
外接圆的方程.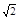
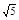
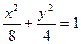 的左右焦点为
的左右焦点为 ;直线
;直线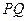 经过
经过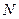 交椭圆于
交椭圆于 两点.
两点.
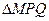 的周长为定值.
的周长为定值.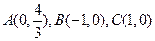 ,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。
,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。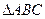 的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。
的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。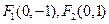 ,一条准线为
,一条准线为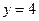 的椭圆上,且
的椭圆上,且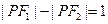 ,
,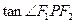 ____________。
____________。
 与抛物线
与抛物线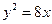 有 一个公共的焦点
有 一个公共的焦点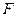 ,且两曲线的一个交点为
,且两曲线的一个交点为 ,若
,若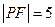 ,则双曲线方程为 .
,则双曲线方程为 .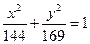 有共同焦点,且过点
有共同焦点,且过点 的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。
的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。