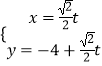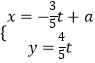��Ŀ����
����Ŀ��Ϊ�˽�ϲ�������˶��Ƿ����Ա��йأ�ij����������ɷ�50��·�ˣ���������������������Ƴ��±���
���䣨�꣩ | [15��25�� | [25��35�� | [35��45�� | [45��55�� | [55��65�� | [65��75�� |
Ƶ�� | 5 | 10 | 8 | 10 | 5 | 5 |
ϲ������ | 4 | 6 | 6 | 3 | 3 |
��1���ڵ���Ľ���У�ϲ�������˶���Ů����10�ˣ���ϲ�������˶���������5�ˣ��뽫�����2��2�������������������ж��ܷ��ڷ�����ĸ��ʲ�����0.005��ǰ������Ϊϲ�������˶����Ա��йأ�˵��������ɣ�
ϲ�������˶� | ��ϲ�������˶� | �ϼ� | |
���� | 5 | ||
�� | 10 | ||
�ϼ� | 50 |
��2������������[15��25����[25��35���ı��������и����ѡȡ���˽����ٵ��飬��ѡ�е�4���в�ϲ�������˶�������ΪX�����������X�ķֲ��к���ѧ������ ������ٽ�ֵ�����ο���
P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽ��K2= ![]() ������n=a+b+c+d��
������n=a+b+c+d��
���𰸡�
��1���⣺����Ƶ�ʷֲ���֪��ϲ�������˶�������Ϊ30����ϲ�������˶�������Ϊ20��
��д2��2���������£�
ϲ�������˶� | ��ϲ�������˶� | �ϼ� | |
���� | 20 | 5 | 25 |
�� | 10 | 15 | 25 |
�ϼ� | 30 | 20 | 50 |
���������������ݣ�����
K2= ![]() =
= ![]() =3��7.879��
=3��7.879��
�����ٽ�ֵ֪���ڷ�����ĸ��ʲ�����0.005��ǰ���£�������Ϊϲ�������˶����Ա��йأ�
��2���⣺��������[15��25����[25��35���ı��������и����ѡȡ���˽����ٵ��飬
��ѡ�е�4���в�ϲ�������˶�������ΪX��
�������X=0��1��2��3��
P��X=0��= ![]()
![]() =
= ![]() ��
��
P��X=1��= ![]()
![]() +
+ ![]()
![]() =
= ![]() ��
��
P��X=2��= ![]()
![]() +
+ ![]()
![]() =
= ![]() ��
��
P��X=3��= ![]()
![]() =
= ![]() ��
��
��X�ķֲ����ǣ�
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
��X����ѧ����EX=0�� ![]() +1��
+1�� ![]() +2��
+2�� ![]() +3��
+3�� ![]() =
= ![]()
����������1������Ƶ�ʷֲ���������ϲ�������˶��Ͳ�ϲ�������˶�����������д������������K2�������ٽ�ֵ�ó����ۣ���2����������֪�������X�Ŀ���ȡֵ�������Ӧ�ĸ���ֵ��д���ֲ��У�������ѧ����ֵ��

����Ŀ��ijũ����������50Ķ����Щ�ؿ������ϡ��������ף���Щũ����ÿĶ������������Ԥ�Ʋ�ֵ���±�������ũ����20���Ͷ�����Ӧ�����ƻ�����ʹÿĶ�ض�����������(���ױ���)�������Ͷ����������Ź���(ÿ���Ͷ���ֻ����ֲһ������)������Ԥ���ܲ�ֵ����ߣ�
���� | ����/Ķ | ��ֵ/Ķ |
���� | 1/2 | 0.6��Ԫ |
�� | 1/3 | 0.5��Ԫ |
���� | 1/4 | 0.3��Ԫ |