题目内容
【题目】已知极点与直角坐标系的原点重合，极轴与x轴的正半轴重合，圆C的极坐标是ρ=2asinθ，直线l的参数方程是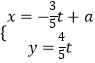 
（t为参数）．
（1）若a=2，M为直线l与x轴的交点，N是圆C上一动点，求|MN|的最大值；
（2）若直线l被圆C截得的弦长为 
，求a的值．
【答案】
（1）解：直线l的参数方程是 
，a=2时，化为普通方程： 
（x﹣2）．令y=0，解得x=2，可得M（2，0）．圆C的极坐标是ρ=2asinθ，即ρ2=4ρsinθ，可得直角坐标方程：x2+y2﹣4y=0，即x2+（y﹣2）2=4．
|MC|=2 
，∴|MN|的最大值为2 +2．
（2）解：圆C的方程为：x2+（y﹣a）2=a2，直线l的方程为：4x+3y﹣4a=0，
圆心C到直线l的距离d= 
= 
．
∴ 
=2 
，解得a= 
【解析】（1）直线l的参数方程是 
，a=2时，化为普通方程： 
（x﹣2）．可得M（2，0）．圆C的极坐标是ρ=2asinθ，即ρ2=4ρsinθ，利用互化公式可得直角坐标方程，求出|MC|=2 
，可得|MN|的最大值为2 +r．（2）圆C的方程为：x2+（y﹣a）2=a2，直线l的方程为：4x+3y﹣4a=0，利用点到直线的距离公式与弦长公式即可得出．
【题目】执行如图所示的程序框图，则下列说法正确的（ ）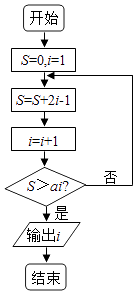 
A.a∈（2，4），输出的i的值为5
B.a∈（4，5），输出的i的值为5
C.a∈（3，4），输出的i的值为5
D.a∈（2，4），输出的i的值为5
【题目】为了解喜好体育运动是否与性别有关，某报记者随机采访50个路人，将调查情况进行整理后制成下表：
年龄（岁） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75） |
频数 | 5 | 10 | 8 | 10 | 5 | 5 |
喜好人数 | 4 | 6 | 6 | 3 | 3 |
（1）在调查的结果中，喜好体育运动的女性有10人，不喜好体育运动的男性有5人，请将下面的2×2列联表补充完整，并判断能否在犯错误的概率不超过0.005的前提下认为喜好体育运动与性别有关？说明你的理由；
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
（2）若从年龄在[15，25），[25，35）的被调查者中各随机选取两人进行追踪调查，记选中的4人中不喜好体育运动的人数为X，求随机变量X的分布列和数学期望． 下面的临界值表供参考：
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：K2= 
，其中n=a+b+c+d）
【题目】为了考察某种中成药预防流感的效果，抽样调查40人，得到如下数据
| 患流感 | 未患流感 |
服用药 | 2 | 18 |
未服用药 | 8 | 12 |
根据表中数据，通过计算统计量K2= 
，并参考以下临界数据：
P（K2＞k0） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
若由此认为“该药物有效”，则该结论出错的概率不超过（ ）
A.0.05
B.0.025
C.0.01
D.0.005