题目内容
已知函数 满足:
满足: (
( ),
),
(1)用反证法证明: 不可能为正比例函数;
不可能为正比例函数;
(2)若 ,求
,求 的值,并用数学归纳法证明:对任意的
的值,并用数学归纳法证明:对任意的 ,均有:
,均有: .
.
(1)主要是考查了反证法的运用,先反设,在推理论证得到矛盾,得出结论。
(2)运用数学归纳法的两步骤来加以证明即可。
解析试题分析: 解:(1)假设 ,代入可得:
,代入可得: 对任意
对任意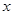 恒成立,故必有
恒成立,故必有 ,但由题设知
,但由题设知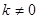 ,故
,故 不可能为正比例函数. 5分
不可能为正比例函数. 5分
(2)由 ,可得:
,可得: ,
, 7分
7分
当 时:显然有
时:显然有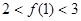 成立.
成立.
假设当 时,仍然有
时,仍然有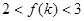 成立.则当
成立.则当 时,
时,
由原式整理可得: =
= . 9分
. 9分
令 ,故
,故
 . 11分
. 11分
故 成立.综上可得:对任意的
成立.综上可得:对任意的 ,均有
,均有 . . 12分
. . 12分
考点:反证法和数学归纳法
点评:主要是考查了反证法以及数学归纳法的运用,属于基础题。

练习册系列答案
相关题目
 的定义域为
的定义域为 .
. 的取值范围;
的取值范围; 的不等式
的不等式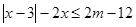 .
. ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 ,试判断
,试判断 是定义在区间
是定义在区间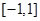 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围; 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 .
. 时,
时, 取得极值,求
取得极值,求 的值;
的值; ,当
,当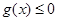 在其定义域内恒成立,并证明
在其定义域内恒成立,并证明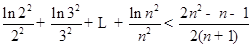 (
( ).
). ,
, )时,f(x)≤g(x),求a的取值范围.
)时,f(x)≤g(x),求a的取值范围.  为有理数且
为有理数且 ),求函数
),求函数 的最小值;
的最小值; :设
:设 为有理数且
为有理数且 时,则
时,则 ;
; ,并证明你的结论;
,并证明你的结论;
 ,
,
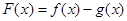 的单调区间;
的单调区间; 时,函数
时,函数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 满足
满足 .求证:
.求证: .
. 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”.
为“一阶比增函数”. 是“一阶比增函数”,求实数
是“一阶比增函数”,求实数 的取值范围;
的取值范围; ,
, ;
; 有解.
有解.  满足
满足 ,其中a>0,a≠1.
,其中a>0,a≠1.
 的值为负数,求
的值为负数,求 的取值范围。
的取值范围。