题目内容
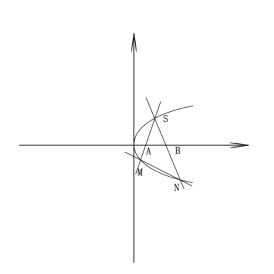
【题目】已知动圆![]() 与直线
与直线![]() 相切且与圆
相切且与圆![]() 外切。
外切。
(1)求圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设第一象限内的点![]() 在轨迹
在轨迹![]() 上,若
上,若![]() 轴上两点
轴上两点![]() ,
,![]() ,满足
,满足![]() 且
且![]() . 延长
. 延长![]() 、
、![]() 分别交轨迹
分别交轨迹![]() 于
于![]() 、
、![]() 两点,若直线
两点,若直线![]() 的斜率
的斜率![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)结合题意,可知圆心P的轨迹为以![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线,建立方程,即可。(2)设出直线SA的方程,代入抛物线方程,用k,m表示M,N的纵坐标,结合
为准线的抛物线,建立方程,即可。(2)设出直线SA的方程,代入抛物线方程,用k,m表示M,N的纵坐标,结合![]() ,计算m,计算S坐标,即可。
,计算m,计算S坐标,即可。
(1)设动圆![]() 的半径为
的半径为![]()
则圆心P到直线![]() 的距离
的距离![]() ,且
,且![]() ,
,
故圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
由抛物线的定义知,圆心![]() 的轨迹是以
的轨迹是以![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线,
为准线的抛物线,
故轨迹![]() 的方程为
的方程为![]() .
.
(另法:设动圆![]() 的半径为
的半径为![]() ,圆心为
,圆心为![]() ,
,
则![]() ,
,![]() ,化简得
,化简得![]() )
)
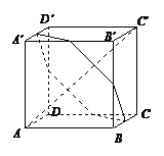
(2)
设![]() ,由
,由![]() ,
,![]() 得,
得,
![]() 的斜率和
的斜率和![]() 的斜率均存在,且互为相反数
的斜率均存在,且互为相反数
设![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() ,
,
联立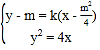 得
得![]() ,
,
故![]() ,
,![]() ,
,
即![]() (*),
(*),
由于![]() 的斜率为
的斜率为![]() ,将(*)中的
,将(*)中的![]() 换成
换成![]() ,
,
得到点![]() 的纵坐标
的纵坐标![]() ,
,
故直线![]() 的斜率
的斜率![]() ,
,
故![]() ,此时
,此时![]() ,
,![]() 时,
时,![]() ,
,
所以点![]() 的坐标为
的坐标为![]()

【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况,随机抽取了一些客户进行回访,调查结果如下表:
汽车型号 | I | II | III | IV | V |
回访客户(人数) | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指:某种型号汽车的回访客户中,满意人数与总人数的比值.
(Ⅰ) 从III型号汽车的回访客户中随机选取1人,则这个客户不满意的概率为________;
(Ⅱ) 从所有的客户中随机选取1个人,估计这个客户满意的概率;
(Ⅲ) 汽车公司拟改变投资策略,这将导致不同型号汽车的满意率发生变化.假设表格中只有两种型号汽车的满意率数据发生变化,那么哪种型号汽车的满意率增加0.1,哪种型号汽车的满意率减少0.1,使得获得满意的客户人数与样本中的客户总人数的比值达到最大?(只需写出结论)