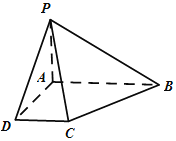
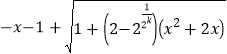题目内容
【题目】有下列命题中错误的是( )
A.![]() 是函数
是函数![]() 的极值点;
的极值点;
B.若![]() ,则
,则![]() ;
;
C.函数![]() 的最小值为2;
的最小值为2;
D.函数![]() 的定义域为[1,2],则函数
的定义域为[1,2],则函数![]() 的定义域为[2,4].
的定义域为[2,4].
【答案】ACD
【解析】
求出函数![]() 的导数确定单调性,判断A;构造函数
的导数确定单调性,判断A;构造函数![]() 判断其单调性,即可判断B;构造函数
判断其单调性,即可判断B;构造函数![]() ,求出函数
,求出函数![]() 的最小值,判断C;由
的最小值,判断C;由![]() 的定义域,利用整体代换求出
的定义域,利用整体代换求出![]() 的定义域,即可判断D.
的定义域,即可判断D.
选项A,![]() 在
在![]() 恒成立,
恒成立,
函数![]() 在
在![]() 单调递增,函数没有极值点,
单调递增,函数没有极值点,
所以A错误;
选项B,设![]() ,
,
![]() 是奇函数,
是奇函数,![]() 为增函数,
为增函数,
所以![]() 为增函数,且
为增函数,且![]() 在
在![]() 处连续,
处连续,
![]() 在
在![]() 单调递增,若
单调递增,若![]() ,则
,则![]() ,
,
即![]() ,所以B成立;
,所以B成立;
选项C,![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 在
在![]() 恒成立,
恒成立,
![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时,
函数取得最小值为![]() ,
,
即函数![]() 的最小值为
的最小值为![]() ,所以C错误;
,所以C错误;
选项D,函数![]() 的定义域为[1,2],
的定义域为[1,2],
函数![]() 的定义域需满足
的定义域需满足![]() ,
,
所以![]() 的定义域是
的定义域是![]() ,所以D错误.
,所以D错误.
故选:ACD

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
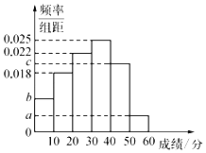
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: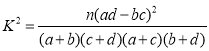 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |