题目内容
抛物线y2=2px与直线ax+y-4=0交于两点A、B,其中点A的坐标为(1,2),设抛物线的焦点为F,则|FA|+|FB|等于( )
A.7 B.3 C.6 D.5
C.6 D.5
A.7 B.3
 C.6 D.5
C.6 D.5A
点A(1,2)是抛物线与直线的交点,∴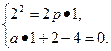 ∴
∴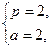
即抛物线方程为y2=4x,直线方程为2x+y-4=0.
由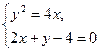 得x2-5x+4=0.
得x2-5x+4=0.
∴x1+x2=5.∴|AF|+|BF|=x1+x2+p=5+2=7.故应选A.
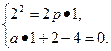 ∴
∴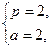
即抛物线方程为y2=4x,直线方程为2x+y-4=0.
由
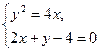 得x2-5x+4=0.
得x2-5x+4=0.∴x1+x2=5.∴|AF|+|BF|=x1+x2+p=5+2=7.故应选A.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
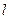 过抛物线的焦点F,交抛物线与A、B两点, 且
过抛物线的焦点F,交抛物线与A、B两点, 且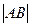 ="4p" ,求直线
="4p" ,求直线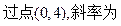 -1的直线与抛物线
-1的直线与抛物线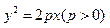 交于两点A,B,如果
交于两点A,B,如果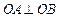 (O为原点)求P的值及抛物线的焦点坐标。
(O为原点)求P的值及抛物线的焦点坐标。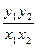 的值为________________.
的值为________________.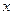 轴上的抛物线被直线
轴上的抛物线被直线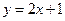 截得的弦长为
截得的弦长为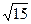 ,
,