题目内容
7.设f(x)是定义在实数集R上的函数,满足条件y=f(x+1)是偶函数,且当x≥1时,f(x)=($\frac{1}{2}$)x-1,则f($\frac{2}{3}$),f($\frac{3}{2}$),f($\frac{1}{3}$)的大小关系是( )| A. | f($\frac{2}{3}$)>f($\frac{3}{2}$)>f($\frac{1}{3}$) | B. | f($\frac{2}{3}$)>f($\frac{1}{3}$)>f($\frac{3}{2}$) | C. | f($\frac{3}{2}$)>f($\frac{3}{2}$)>f($\frac{1}{3}$) | D. | f($\frac{1}{3}$)>f($\frac{3}{2}$)>f($\frac{2}{3}$) |
分析 根据函数y=f(x+1)是偶函数得到函数关于x=1对称,然后利用函数单调性和对称之间的关系,进行比较即可得到结论.
解答 解:∵y=f(x+1)是偶函数,
∴f(-x+1)=f(x+1),
即函数f(x)关于x=1对称.
∵当x≥1时,f(x)=($\frac{1}{2}$)x-1为减函数,
∴当x≤1时函数f(x)为增函数.
∵f($\frac{3}{2}$)=f($\frac{1}{2}$+1)=f(-$\frac{1}{2}$+1)=f($\frac{1}{2}$),且$\frac{1}{3}<\frac{1}{2}<\frac{2}{3}$,
∴f($\frac{2}{3}$)>f($\frac{3}{2}$)>f($\frac{1}{3}$),
故选:A.
点评 本题主要考查函数奇偶性和单调性的应用,根据条件求出函数的对称性是解决本题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
19.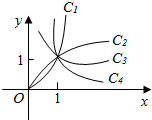 已知幂函数y=xa在第一象限内的图象如图所示,a取±2,±$\frac{1}{2}$四个值,则相应的曲线C1,C2,C3,C4的a的值依次为( )
已知幂函数y=xa在第一象限内的图象如图所示,a取±2,±$\frac{1}{2}$四个值,则相应的曲线C1,C2,C3,C4的a的值依次为( )
 已知幂函数y=xa在第一象限内的图象如图所示,a取±2,±$\frac{1}{2}$四个值,则相应的曲线C1,C2,C3,C4的a的值依次为( )
已知幂函数y=xa在第一象限内的图象如图所示,a取±2,±$\frac{1}{2}$四个值,则相应的曲线C1,C2,C3,C4的a的值依次为( )| A. | -2,-$\frac{1}{2}$,$\frac{1}{2}$,2 | B. | 2,$\frac{1}{2}$,-$\frac{1}{2}$,-2 | C. | -$\frac{1}{2}$,-2,2,$\frac{1}{2}$ | D. | 2,$\frac{1}{2}$,-2,-$\frac{1}{2}$ |