题目内容
14.已知sinα-3cosα=0,求$\frac{1}{3}$sin2α+4cos2α的值.分析 利用同角三角函数的基本关系式化简表达式为正切函数的形式,求解即可.
解答 解:sinα-3cosα=0,可得tanα=3.
$\frac{1}{3}$sin2α+4cos2α=$\frac{\frac{1}{3}{sin}^{2}α+4{cos}^{2}α}{{sin}^{2}α+{cos}^{2}α}$=$\frac{\frac{1}{3}{tan}^{2}α+4}{{tan}^{2}α+1}$=$\frac{7}{10}$.
故答案为:$\frac{7}{10}$.
点评 本题考查三角函数的化简求值,考查计算能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
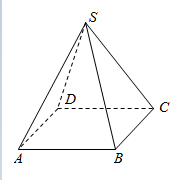 如图,在正四棱锥S-ABCD中,底面边长为6cm,侧棱长为3$\sqrt{5}$cm.
如图,在正四棱锥S-ABCD中,底面边长为6cm,侧棱长为3$\sqrt{5}$cm.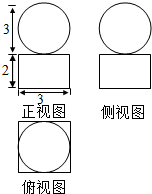 设如图是某几何体的三视图,求该几何体的体积和表面积.
设如图是某几何体的三视图,求该几何体的体积和表面积.