题目内容
15.求垂直于直线3x-2y+4=0,且过直线2x-3y+1=0和3x-4y-2=0的交点的直线方程.分析 联立$\left\{\begin{array}{l}{2x-3y+1=0}\\{3x-4y-2=0}\end{array}\right.$,解得P.设垂直于直线3x-2y+4=0的方程为2x+3y+m=0,把P代入上述方程即可得到.
解答 解:联立$\left\{\begin{array}{l}{2x-3y+1=0}\\{3x-4y-2=0}\end{array}\right.$,解得P(10,7).
设垂直于直线3x-2y+4=0的方程为2x+3y+m=0,
把P(10,7)代入上述方程可得:20+21+m=0,解得m=-41.
∴要求的直线方程为:2x+3y-41=0.
点评 本题考查了相互垂直的直线斜率之间的关系、直线的交点,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
2.下列变量间的关系属于线性关系的是( )
| A. | 球的体积与表面积之间的关系 | |
| B. | 正方形面积和它的边长之间的关系 | |
| C. | 家庭收入愈多,其消费支出也有增长的趋势 | |
| D. | 价格不变的条件下,商品销售额与销量量之间的关系 |
7.容量为20的样本数据,分组后的频数如下表:
则样本数据落在区间[40,70)的频率为( )
| 分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
| A. | 0.35 | B. | 0.45 | C. | 0.55 | D. | 0.65 |
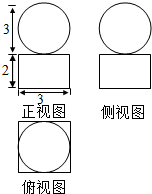 设如图是某几何体的三视图,求该几何体的体积和表面积.
设如图是某几何体的三视图,求该几何体的体积和表面积.