题目内容
10.(1)若f(x)=sinxcos2x,则f′(x)=cosxcos2x-2sinxsin2x;(2)若f(x)=exsin$\frac{1}{2}$x,则f′(x)=exsin$\frac{1}{2}$x+$\frac{1}{2}$excosx$\frac{1}{2}$x.
分析 根据复合函数的导数公式进行求导即可.
解答 解:(1)若f(x)=sinxcos2x,
则f′(x)=cosxcos2x+sinx(-sin2x•2)=cosxcos2x-2sinxsin2x;
(2)若f(x)=exsin$\frac{1}{2}$x,则f′(x)=exsin$\frac{1}{2}$x+excosx$\frac{1}{2}$x•$\frac{1}{2}$=exsin$\frac{1}{2}$x+$\frac{1}{2}$excosx$\frac{1}{2}$x,
故答案为:cosxcos2x-2sinxsin2x;exsin$\frac{1}{2}$x+$\frac{1}{2}$excosx$\frac{1}{2}$x
点评 本题主要考查导数的计算,要求熟练掌握掌握常见函数的导数公式,比较基础.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
2.下列变量间的关系属于线性关系的是( )
| A. | 球的体积与表面积之间的关系 | |
| B. | 正方形面积和它的边长之间的关系 | |
| C. | 家庭收入愈多,其消费支出也有增长的趋势 | |
| D. | 价格不变的条件下,商品销售额与销量量之间的关系 |
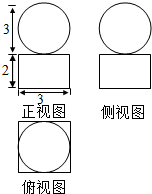 设如图是某几何体的三视图,求该几何体的体积和表面积.
设如图是某几何体的三视图,求该几何体的体积和表面积.