题目内容
4.已知a,b,c为锐角△ABC的内角A,B,C的对边,满足acosA+bcosB=c,(1)证明:△ABC为等腰三角形;
(2)若△ABC的外接圆面积为π,求$\frac{3{b}^{2}+b+4c}{a}$的范围.
分析 (1)利用余弦定理表示出cosA与cosB,代入已知等式整理得到a=b,即可得证;
(2)设三角形ABC外接圆半径为R,由圆的面积公式求出R的值,所求式子利用正弦定理化简,整理为一个角的正弦函数,由正弦函数的值域确定出范围即可.
解答 (1)证明:由acosA+bcosB=c,利用余弦定理化简得:a•$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$+b•$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=c,
整理得:a2(b2+c2-a2)+b2(a2+c2-b2)=2abc2,即(a-b)2[c2-(a+b)2]=0,
∵c<a+b,∴c2≠(a+b)2,
∴a=b,
则△ABC为等腰三角形;
(2)解:设△ABC的外接圆半径为R,由πR2=π,得到R=1,
由(1)得:A=B,
由正弦定理得:$\frac{3{b}^{2}+b+4c}{a}$=$\frac{12{R}^{2}si{n}^{2}B+2RsinB+8RsinC}{2RsinA}$=$\frac{6si{n}^{2}B+sinB+8sinBcosB}{sinB}$=6sinB+1+8cosB=10sin(B+θ)+1,
记为f(B),其中sinθ=$\frac{4}{5}$>$\frac{\sqrt{2}}{2}$,cosθ=$\frac{3}{5}$,且θ∈($\frac{π}{4}$,$\frac{π}{2}$),
∵△ABC为锐角三角形,
∴$\left\{\begin{array}{l}{0<A<\frac{π}{2}}\\{0<B<\frac{π}{2}}\\{0<C=π-A-B<\frac{π}{2}}\end{array}\right.$,
结合A=B,得到$\frac{π}{4}$<B<$\frac{π}{2}$,
∴B+θ∈($\frac{π}{2}$,π),
∴f(B)在$\frac{π}{4}$<B<$\frac{π}{2}$上单调递减,
当B=$\frac{π}{2}$时,f(B)=10sin($\frac{π}{2}$+θ)+1=10cosθ+1=7;
当B=$\frac{π}{4}$时,f(B)=10sin($\frac{π}{4}$+θ)+1=10×$\frac{\sqrt{2}}{2}$(sinθ+cosθ)+1=7$\sqrt{2}$+1,
∴f(B)∈(7,7$\sqrt{2}$+1),即$\frac{3{b}^{2}+b+4c}{a}$∈(7,7$\sqrt{2}$+1).
点评 此题考查了正弦、余弦定理,以及正弦函数的定义域与值域,熟练掌握定理是解本题的关键.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
| A. | 3-2 | B. | 0.3-2 | C. | log0.32 | D. | 无法确定 |
| A. | $\sqrt{5}$ | B. | $2\sqrt{5}$ | C. | $3\sqrt{5}$ | D. | 0 |
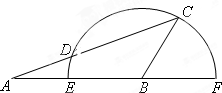 如图,在△ABC中,AB=5,BC=3,∠ABC=120°,以点B为圆心,线段BC的长为半径的半圆交AB所在直线于点E、F,交线段AC于点D,则线段AD的长为$\frac{16}{7}$.
如图,在△ABC中,AB=5,BC=3,∠ABC=120°,以点B为圆心,线段BC的长为半径的半圆交AB所在直线于点E、F,交线段AC于点D,则线段AD的长为$\frac{16}{7}$.