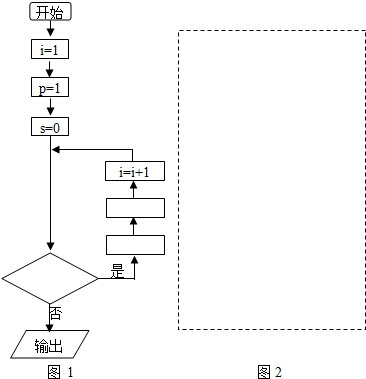
题目内容
14.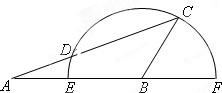 如图,在△ABC中,AB=5,BC=3,∠ABC=120°,以点B为圆心,线段BC的长为半径的半圆交AB所在直线于点E、F,交线段AC于点D,则线段AD的长为$\frac{16}{7}$.
如图,在△ABC中,AB=5,BC=3,∠ABC=120°,以点B为圆心,线段BC的长为半径的半圆交AB所在直线于点E、F,交线段AC于点D,则线段AD的长为$\frac{16}{7}$.
分析 由余弦定理得AC=7,AE=5-3=2,AF=5+3=8,由相交弦定理得AD•AC=AE•AF,由此能求出AD.
解答 解: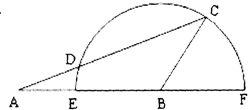 如图,∵在△ABC中,AB=5,BC=3,∠ABC=120°,
如图,∵在△ABC中,AB=5,BC=3,∠ABC=120°,
∴AC=$\sqrt{25+9-2×5×3×cos120°}$=7,
∵以点B为圆心,线段BC的长为半径的半圆
交AB所在直线于点E、F,交线段AC于点D,
∴AE=5-3=2,AF=5+3=8,
∴AD•AC=AE•AF,
∴AD=$\frac{AE•AF}{AC}$=$\frac{16}{7}$,
故答案为:$\frac{16}{7}$.
点评 本题考查线段长的求法,是中档题,合理运用相交弦定理和余弦定理是关键.

练习册系列答案
相关题目
19.假设在3.0秒内的任何时间,两条不相关的短信机会均等地进入同一部手机,若这两条短信进入手机的时间之差小1.0秒,手机就会受到干扰,则手机受到干扰的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{9}$ |
3.点P在直线a上,直线a在平面α内可记为( )
| A. | P∈a,a?α | B. | P?a,a?α | C. | P?a,a∈α | D. | P∈a,a∈α |
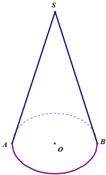 如图,已知圆锥S0的母线SA的长度为2,一只蚂蚁从点B绕着圆锥侧面爬回点B的最短距离为2,则圆锥SO的底面半径为$\frac{1}{3}$.
如图,已知圆锥S0的母线SA的长度为2,一只蚂蚁从点B绕着圆锥侧面爬回点B的最短距离为2,则圆锥SO的底面半径为$\frac{1}{3}$.