题目内容
【题目】数列{an}的前n项和Sn=3n2+2n+1.
(1)求{an}的通项公式;
(2)令bn=an2n , 求{bn}的前n项和Tn .
【答案】
(1)解:∵Sn=3n2+2n+1,
∴当n≥2时,an=Sn﹣Sn﹣1=3n2+2n+1﹣[3(n﹣1)2+2(n﹣1)+1]=6n﹣1,
当n=1时,a1=6,不适合上式,
∴an= ![]()
(2)解:∵bn=an2n,
∴n=1时,T1=b1=a1×2=12…..(5分)
n>1时,Tn=6×2+11×22+17×23+…+(6n﹣1)×2n,①
2Tn=6×22+11×23+17×24+…+(6n﹣7)×2n+(6n﹣1)2n+1,②
②﹣①得:Tn=﹣32﹣6(23+24+…+2n)+(6n﹣1)2n+1
=16+(6n﹣7)×2n+1.…..(11分)
∴Tn= ![]()
【解析】(1)由Sn=3n2+2n+1知,当n≥2时,an=Sn﹣Sn﹣1=6n﹣1,验证n=1时是否适合,即可求得{an}的通项公式;(2)bn=an2n , 易求T1=12,n>1时,Tn=6×2+11×22+17×23+…+(6n﹣1)×2n , 利用错位相减法可求得{bn}的前n项和Tn .
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系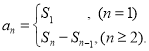 .
.

练习册系列答案
相关题目

