Question

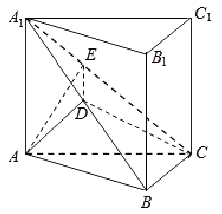
【题目】如图，在直三棱柱 中，平面 侧面 ，且 ．
（1）求证： ；
（2）若直线 与平面 所成角的大小为 ，求锐二面角 的大小．

Answer 1

【答案】
（1）如图，取 的中点D，连接AD，

因为 ,所以 ,

由平面 ⊥侧面 ,且平面 ，

得AD⊥平面 ，

又BC 平面 ，所以AD⊥BC，

因为三棱柱 是直三棱柱，则 ⊥底面ABC，

所以

又 ，从而BC⊥侧面 ，又AB 侧面 ，

故AB⊥BC.

（2）连接CD，由（1）可知AD⊥平面 ，则CD是AC在平面 内的射影，

∴∠ACD即为直线AC与平面 所成的角，则∠ACD=30°.

在等腰直角 中， ，且点D是 的中点，

∴ ,又 ，∠ACD=30°，∴AC= .

过点A作AE⊥ 于点E，连接DE，由（1）知AD⊥平面 ，则 ,又 ,

∴ ,

∴∠AED即为二面角 的一个平面角.

在直角△ 中， ，

又 ，

∴ ,

又二面角 为锐二面角，∴∠AED=60°，

即二面角 的大小为60°.

【解析】本小题主要考查线线垂直，线面垂直，二面角等基础知识，考查推理论证能力、运算求解能力、空间想象能力，并考查应用向量知识解决立体几何问题的能力．
【考点精析】掌握直线与平面垂直的判定是解答本题的根本，需要知道一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．