Question

【题目】若函数f（x）= x3+ax2+bx+c有极值点x1 ， x2（x1＞x2），f（x1）=x1 ， 则关于x的方程[f（x）]2+2af（x）+b=0的不同实数根的个数是 ．

Answer 1

【答案】3
【解析】解：对f（x）求导得：f'（x）=x2+2ax+b；
f（x）有极值点x1 ， x2 对应于f'（x）=0的两个零点；
关于x的方程[f（x）]2+2af（x）+b=0，则有f（x）=x1 或 f（x）=x2；
由图形知y=x1 与f（x）有2个交点；
∵x1＞x2 ， 故y=x2 与f（x）有1个交点；
所以答案是：3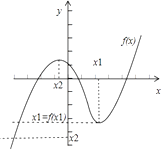

【考点精析】本题主要考查了函数的极值与导数的相关知识点，需要掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值才能正确解答此题．