��Ŀ����
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AC=BC=a����P�ڱ�AB�ϣ��� ![]() =��
=�� ![]() ���ˣ�0��������P��PE��BC��AC��E����PF��AC��BC��F����PE����APE���۳ɡ�A��PE��ʹƽ��A��PE��ƽ��ABC����PF����BPF���۳ɡ�B��PF��ʹƽ��B��PF��ƽ��ABC��
���ˣ�0��������P��PE��BC��AC��E����PF��AC��BC��F����PE����APE���۳ɡ�A��PE��ʹƽ��A��PE��ƽ��ABC����PF����BPF���۳ɡ�B��PF��ʹƽ��B��PF��ƽ��ABC�� 
��1����֤��B��C��ƽ��A��PE��
��2���Ƿ������ʵ���ˣ�ʹ�ö����C��A��B�䩁P�Ĵ�СΪ60�㣿�����ڣ�����˵�ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��֤������FC��PE��FCƽ��A'PE����FC��ƽ��A'PE��
��ƽ��A'PE��ƽ��ABC����A'E��PE����A'E��ƽ��ABC��
ͬ����B'F��ƽ��ABC����B'F��A'E���Ӷ�B'F��ƽ��A'PE��
��ƽ��B'CF��ƽ��A'PE���Ӷ�B'C��ƽ��A'PE��
��2���⣺������ʵ����= ![]() ��ʹ�ö����C��A��B�䩁P�Ĵ�СΪ60�㣮
��ʹ�ö����C��A��B�䩁P�Ĵ�СΪ60�㣮
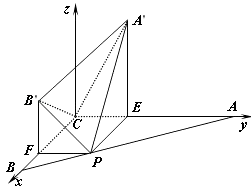
��ʵ�ϣ���CΪԭ�㣬CB����ֱ��Ϊx�ᣬCA����ֱ��Ϊy�ᣬ��C�Ҵ�ֱ��ƽ��ABC��ֱ��Ϊz�ᣬ�����ռ�ֱ������ϵ����ͼ��
��AC=BC=a���� ![]() =��
=�� ![]() ���ˣ�0����
���ˣ�0����
��C��0��0��0����A�䣨0�� ![]() ��
�� ![]() ����B�䣨
����B�䣨 ![]() ��0��
��0�� ![]() ����P��
����P�� ![]() ��
�� ![]() ��0����
��0����
�� ![]() =��0��
=��0�� ![]() ��
�� ![]() ����
���� ![]() =��
=�� ![]() ����
���� ![]() ��
�� ![]() ����
���� ![]() =��0��
=��0�� ![]() ����
���� ![]() ����
����
ƽ��CA'B'��һ�������� ![]() =��
=�� ![]() ���ˣ���1����ƽ��PA'B'��һ��������
���ˣ���1����ƽ��PA'B'��һ�������� ![]() =��1��1��1����
=��1��1��1����
�� ![]() =
=  =cos60��=
=cos60��= ![]() ��
��
����� ![]() ��8��+9=0����æ�=
��8��+9=0����æ�= ![]() ��
��
�������ʵ����= ![]() ��ʹ�ö����C��A��B�䩁P�Ĵ�СΪ60�㣮
��ʹ�ö����C��A��B�䩁P�Ĵ�СΪ60�㣮
����������1����������ƽ�е��ж���������֤��FC��ƽ��A'PE�����������洹ֱ�����ʶ�������֤��B��F��A��E�������õ�B'F��ƽ��A'PE����������ƽ�е��ж��������ɵõ� ƽ��B'CF��ƽ��A'PE���Ӷ��õ�����ƽ�У���2��ͨ�������ռ�ֱ������ϵ������֪��� ![]() =��
=�� ![]() ���ˣ�0��������õ�����꣬�Ѷ����C��A��B�䩁P�Ĵ�СΪ60��ת��Ϊ����ƽ��ķ������ļн���ʽ��æ˵�ֵ��
���ˣ�0��������õ�����꣬�Ѷ����C��A��B�䩁P�Ĵ�СΪ60��ת��Ϊ����ƽ��ķ������ļн���ʽ��æ˵�ֵ��
�����㾫��������ֱ����ƽ��ƽ�е��ж�����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪ƽ����һ��ֱ�����ƽ���ڵ�һ��ֱ��ƽ�У����ֱ�����ƽ��ƽ�У����Ϊ������ƽ�У�������ƽ�У�

 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д� ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�