题目内容
9.证明:$\sqrt{5}$-$\sqrt{10}$>$\sqrt{3}$$-\sqrt{8}$.分析 分析使不等式$\sqrt{5}$-$\sqrt{10}$>$\sqrt{3}$$-\sqrt{8}$成立的充分条件,一直分析到使不等式成立的充分条件显然具备,从而不等式得证.
解答 证明:要证明:$\sqrt{5}$-$\sqrt{10}$>$\sqrt{3}$$-\sqrt{8}$,
只要证明$\sqrt{5}$+$\sqrt{8}$>$\sqrt{3}$+$\sqrt{10}$,
只要证明:13+2$\sqrt{40}$>13+2$\sqrt{30}$,
只要证明:$\sqrt{40}$>$\sqrt{30}$,
只要证明:40>30,
显然成立,
∴$\sqrt{5}$-$\sqrt{10}$>$\sqrt{3}$$-\sqrt{8}$.
点评 本题主要考查利用分析法证明不等式,利用用分析法证明不等式的关键是寻找使不等式成立的充分条件,直到使不等式成立的充分条件已经显然具备为止,属于中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
4.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{-2x},x≤-1}\\{ax+3,x>-1}\end{array}\right.$为单调函数,则实数a的取值范围是( )
| A. | (-1,0] | B. | [-1,0) | C. | (-1,0) | D. | (-∞,-1] |
1.已知A=$\frac{sin(kπ-α)cos[(k-1)π-α]}{sin[(k+1)π+α]cos(kπ+α)}$(k∈Z),则该值构成的集合是( )
| A. | {1,-1,2,-2} | B. | {-1,1} | C. | {-1} | D. | {1,-1,0,2,-2} |
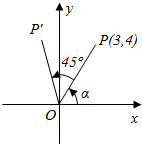 如图所示,角α终边上一点P的坐标是(3,4),将OP绕原点旋转45°到OP′的位置.试求点P′的坐标.
如图所示,角α终边上一点P的坐标是(3,4),将OP绕原点旋转45°到OP′的位置.试求点P′的坐标.