题目内容
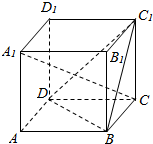
11.证明:长方体的四条体对角线交于一点,且这点为其外接球的球心.分析 以下底面ABCD的顶点A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,AA1所在直线为z轴,建立坐标系,由中点坐标公式可以求得A1C,AC1,BD1,B1D的中点都是($\frac{1}{2}a$,$\frac{1}{2}b$,$\frac{1}{2}c$),即可证明结论.
解答 证明:以下底面ABCD的顶点A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,AA1所在直线为z轴,建立坐标系,设长AD=a,宽AB=b,高AA1=c
则可分别求得A(0,0,0),B(b,0,0),C(b,a,0),D(0,a,0),A1(0,0,c),B1(b,0,c),C1(b,a,c),D1(0,a,c),
由中点坐标公式可以求得A1C,AC1,BD1,B1D的中点都是($\frac{1}{2}a$,$\frac{1}{2}b$,$\frac{1}{2}c$),
所以长方体的四条对角线交于一点,且这点为其外接球的球心.
点评 本题考查利用空间坐标系证明几何问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
3.集合A={x|$\frac{x+1}{x-2}$≥0},B={y|y=sin$\frac{nπ}{2}$,n∈N},则(∁RA)∩B=( )
| A. | {-1,0,1} | B. | {-1,1} | C. | {0,1} | D. | {-1} |
20.已知两条直线l1:x+m2y+12=0和l2:(m-2)x+3my+4m=0,则l1∥l2是m=-1的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
 棱长为1的正方体AC1中,求证:A1C⊥平面BDC1.
棱长为1的正方体AC1中,求证:A1C⊥平面BDC1.