题目内容
17.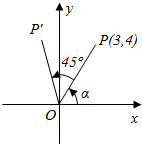 如图所示,角α终边上一点P的坐标是(3,4),将OP绕原点旋转45°到OP′的位置.试求点P′的坐标.
如图所示,角α终边上一点P的坐标是(3,4),将OP绕原点旋转45°到OP′的位置.试求点P′的坐标.
分析 利用两角和的正弦函数以及余弦函数即可求点P′的坐标.
解答 解:∵角α终边上一点P的坐标是(3,4),
∴32+42=52,
∴|OP|=5,
∴sinα=$\frac{4}{5}$,cosα=$\frac{3}{5}$,
设p′的坐标为(x,y),
∴y=|OP′|sin(α+45°)=5(sinαcos45°+cosαsin45°)=5($\frac{4}{5}$×$\frac{\sqrt{2}}{2}$+$\frac{3}{5}$×$\frac{\sqrt{2}}{2}$)=$\frac{7\sqrt{2}}{2}$,
x=|OP′|cos(α+45°)=5(cosαcos45°-sinαsin45°)=5($\frac{3}{5}$×$\frac{\sqrt{2}}{2}$-$\frac{4}{5}$×$\frac{\sqrt{2}}{2}$)=-$\frac{\sqrt{2}}{2}$,
∴p′的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{7\sqrt{2}}{2}$).
点评 本题考查向量与三角函数的相结合,两角和与差的三角函数的应用,考查计算能力.

练习册系列答案
相关题目
8.已知二次函数f(x)=m2x2+2mx-3,则下列结论正确的是 ( )
| A. | 函数f(x)有最大值-4 | B. | 函数f(x)有最小值-4 | ||
| C. | 函数f(x)有最大值-3 | D. | 函数f(x)有最小值-3 |
5.已知等差数列的首项a1=2,公差d=-2,前n项的和Sn=-70,则n=( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |