题目内容
已知圆C和 轴相切,圆心C在直线
轴相切,圆心C在直线 上,且被直线
上,且被直线 截得的弦长为
截得的弦长为 ,求圆C的方程.
,求圆C的方程.
(x-3)2+(y-1)2=9或(x+3)2+(y+1)2=9;
解析试题分析:由圆心C在直线 上,可设设圆心坐标为(3m,m),又圆C和y轴相切,得圆的半径为3|m|,根据圆心到直线y=x的距离为
上,可设设圆心坐标为(3m,m),又圆C和y轴相切,得圆的半径为3|m|,根据圆心到直线y=x的距离为 ,化简求出m,即而求出圆C的方程.
,化简求出m,即而求出圆C的方程.
试题解析:设圆心坐标为(3m,m). 2分
∵圆C和y轴相切,得圆的半径为3|m|, 4分
∴圆心到直线y=x的距离为 . 6分
. 6分
由半径、弦心距、半弦长的关系得9m2=7+2m2, 8分
∴m=±1, 10分
∴所求圆C的方程为
(x-3)2+(y-1)2=9或(x+3)2+(y+1)2=9. 12分
考点:1.圆的方程;2.点到直线距离公式.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 +y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.
+y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点. 经过点
经过点 和
和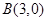 ,且圆心在直线
,且圆心在直线 上.
上.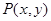 为圆
为圆 到直线
到直线 的距离的最大值和最小值.
的距离的最大值和最小值. 与圆
与圆 外切于点
外切于点 ,直线
,直线 是两圆的外公切线,分别与两圆相切于
是两圆的外公切线,分别与两圆相切于 两点,
两点, 是圆
是圆 作圆
作圆 .
.
 三点共线;
三点共线; .
. 的左右顶点分别为
的左右顶点分别为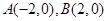 ,离心率
,离心率 .过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
.过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且 .
. 交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.
交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.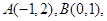 动点P满足
动点P满足 .
.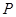 的轨迹为曲线
的轨迹为曲线 ,求此曲线的方程;
,求此曲线的方程; 在直线
在直线 :
: 上,直线
上,直线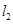 经过点
经过点 ,求
,求 的最小值.
的最小值.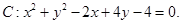 问在圆C上是否存在两点A,B关于直线
问在圆C上是否存在两点A,B关于直线 对称,且以AB为直径的圆经过原点?若存在,写出直线AB的方程,若不存在,说明理由.
对称,且以AB为直径的圆经过原点?若存在,写出直线AB的方程,若不存在,说明理由. 中,圆
中,圆 的参数方程为
的参数方程为 (
(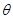 为参数),以
为参数),以 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.