题目内容
【题目】己知椭圆![]() 的焦距为
的焦距为![]() ,以椭圆C的右顶点A为圆心的圆与直线
,以椭圆C的右顶点A为圆心的圆与直线![]() 相交于P,Q两点,且
相交于P,Q两点,且![]() .
.
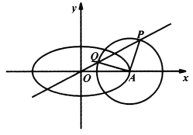
(I)求椭圆C的标准方程和圆A的方程。
(II)不过原点的直线l与椭圆C交于M,N两点,已知直线OM,l,ON的斜率![]() 成等比数列,记以线段OM,线段ON为直径的圆的面积分别为
成等比数列,记以线段OM,线段ON为直径的圆的面积分别为![]() 的值是否为定值?若是,求出此值:若不是,说明理由.
的值是否为定值?若是,求出此值:若不是,说明理由.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)答案见解析.
;(Ⅱ)答案见解析.
【解析】
分析:(1)设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则![]()
![]() ,所以
,所以![]()
![]() ,又
,又![]() ,所以
,所以![]() ,从而易得关于a,b的方程组,即可得到所求椭圆方程和圆的方程.
,从而易得关于a,b的方程组,即可得到所求椭圆方程和圆的方程.
(2)设直线l的方程为y=kx+m,代入椭圆方程,消去y,根据k1、k、k2恰好构成等比数列,求出k,进而表示出![]() ,即可得出结论.
,即可得出结论.
详解:(1)如图,设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则![]()
![]() ,
,
因为![]() ,即
,即![]()
![]() ,所以
,所以![]()
![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]()
![]() ,所以
,所以![]() .
.
由已知得![]() ,所以
,所以![]()
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() ,
,
![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以圆![]() 的方程为
的方程为![]() .
.
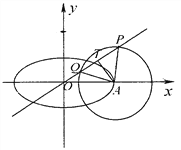
(2)设直线![]() 的方程为
的方程为![]() ,
,![]()
由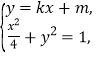 ,得
,得![]() ,
,
所以![]() ,由题设知
,由题设知![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
则![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
故![]() 为定值,该定值为
为定值,该定值为![]() .
.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】手机是人们必不可少的工具,极大地方便了人们的生活、工作、学习,现代社会的衣食住行都离不开它.某调查机构调查了某地区各品牌手机的线下销售情况,将数据整理得如下表格:
品牌 |
|
|
|
|
|
| 其他 |
销售比 |
|
|
|
|
|
|
|
每台利润(元) | 100 | 80 | 85 | 1000 | 70 | 200 |
该地区某商场岀售各种品牌手机,以各品牌手机的销售比作为各品牌手机的售出概率.
(1)此商场有一个优惠活动,每天抽取一个数字![]() (
(![]() ,且
,且![]() ),规定若当天卖出的第
),规定若当天卖出的第![]() 台手机恰好是当天卖出的第一台
台手机恰好是当天卖出的第一台![]() 手机时,则此
手机时,则此![]() 手机可以打5折.为保证每天该活动的中奖概率小于0.05,求
手机可以打5折.为保证每天该活动的中奖概率小于0.05,求![]() 的最小值;(
的最小值;(![]() ,
,![]() )
)
(2)此商场中一个手机专卖店只出售![]() 和
和![]() 两种品牌的手机,
两种品牌的手机,![]() ,
,![]() 品牌手机的售出概率之比为
品牌手机的售出概率之比为![]() ,若此专卖店一天中卖出3台手机,其中
,若此专卖店一天中卖出3台手机,其中![]() 手机
手机![]() 台,求
台,求![]() 的分布列及此专卖店当天所获利润的期望值.
的分布列及此专卖店当天所获利润的期望值.

