��Ŀ����
����Ŀ���μӺ�ˮ��ѧ��ѧѡ�ε�ͬѧ����ij��˾��һ�ֲ�Ʒ������۸����ͳ�ƣ��õ��������ݺ�ɢ��ͼ��
���� |
|
|
|
|
|
|
������ |
|
|
|
|
|
|
|
|
|
|
|
|
|
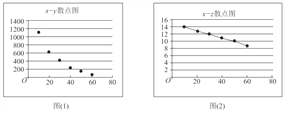
���ο����ݣ�![]()
![]() ��
��
��I������ɢ��ͼ�жϣ�![]() ��
��![]() ��
��![]() ��
��![]() ��һ�Ծ��н�ǿ����������ԣ������жϼ��ɣ�����˵�����ɣ���
��һ�Ծ��н�ǿ����������ԣ������жϼ��ɣ�����˵�����ɣ���
��II�����ݣ�I�����жϽ�������ݣ�����![]() ����
����![]() �Ļع鷽�̣������е�ϵ����������λ��Ч���֣���
�Ļع鷽�̣������е�ϵ����������λ��Ч���֣���
��III������Ϊ����Ԫ/![]() ʱ���������Ԥ��ֵ���
ʱ���������Ԥ��ֵ���
������һ������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��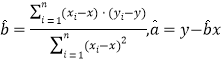 .
.
���𰸡���I����ɢ��ͼ��֪��![]() ��
��![]() ���н�ǿ�����������; ��II��
���н�ǿ�����������; ��II��![]() ; ��III����ֵΪ
; ��III����ֵΪ![]() Ԫ/
Ԫ/![]() ʱ���������Ԥ��ֵ���.
ʱ���������Ԥ��ֵ���.
������������������Ƚ�����ɢ��ͼ���Է���![]() ��
��![]() ���н�ǿ����������ԣ����ñ����ṩ��
���н�ǿ����������ԣ����ñ����ṩ��![]() ��
��![]() �Ķ�Ӧֵ����
�Ķ�Ӧֵ����![]() ����������ṩ���ֳ�����
����������ṩ���ֳ�����![]() �ټ���
�ټ���![]() ���ó�
���ó�![]() ����
����![]() ���ó�
���ó�![]() ��������
��������![]() ����
����![]() ���ó�
���ó�![]() ����
����![]() �Ļع鷽�̣�ע�Ᵽ��С������ʾ�����������ҳ���ֵ.
�Ļع鷽�̣�ע�Ᵽ��С������ʾ�����������ҳ���ֵ.
���������
��I����ɢ��ͼ��֪��![]() ��
��![]() ���н�ǿ�����������.
���н�ǿ�����������.
��II������ã�![]() ��
��
![]() ��
��
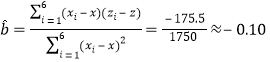 ��
��
��![]() ��
��
��![]() ��
��
�����Իع鷽��Ϊ![]() ��
��
��![]() ����
����![]() �Ļع鷽��Ϊ
�Ļع鷽��Ϊ![]() .
.
��III����������Ϊ![]() ��
��
��![]() ��
��
����![]() ��
��
��![]() �����
�����![]() .
.
�ɺ����ĵ����Կ�֪����![]() ʱ���������Ԥ��ֵ���
ʱ���������Ԥ��ֵ���
�ඨֵΪ![]() Ԫ/
Ԫ/![]() ʱ���������Ԥ��ֵ���.
ʱ���������Ԥ��ֵ���.