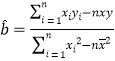题目内容
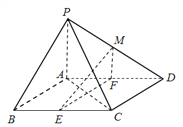
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() ,侧面
,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】试题分析:(Ⅰ)线面垂直的证明,往往利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的寻找与论证,一般从两个方面,一是利用平几知识,如本题经解三角形可得![]() ,再根据中点条件得平行条件,从而可得
,再根据中点条件得平行条件,从而可得![]() .二是利用线面位置关系有关定理进行转化,如本题利用面面垂直的性质定理可得线面垂直,再根据线面垂直性质定理可得线线垂直.(Ⅱ)解决有关线面角的问题,一般利用空间向量数量积进行处理比较方便,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出面的法向量,再根据向量数量积求出直线向量与法向量夹角余弦值,最后根据线面角与向量夹角之间关系列等量关系,求出比值.
.二是利用线面位置关系有关定理进行转化,如本题利用面面垂直的性质定理可得线面垂直,再根据线面垂直性质定理可得线线垂直.(Ⅱ)解决有关线面角的问题,一般利用空间向量数量积进行处理比较方便,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出面的法向量,再根据向量数量积求出直线向量与法向量夹角余弦值,最后根据线面角与向量夹角之间关系列等量关系,求出比值.
试题解析:
(Ⅰ)证明:在平行四边形![]() 中,因为
中,因为![]() ,
, ![]() ,
,
所以![]() .由
.由![]() 分别为
分别为![]() 的中点,得
的中点,得![]() ,
,
所以![]() .
.
因为侧面![]() 底面
底面![]() ,且
,且![]() ,所以
,所以![]() 底面
底面![]() .
.
又因为![]() 底面
底面![]() ,所以
,所以![]() .
.
又因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)解:因为![]() 底面
底面![]() ,
, ![]() ,所以
,所以![]() 两两垂直,
两两垂直,
以![]() 分别为
分别为![]() 、
、![]() 、
、![]() ,建立空间直角坐标系,
,建立空间直角坐标系,
则![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
, ![]() ,易得平面
,易得平面![]() 的法向量
的法向量![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() ,
, ![]() ,得
,得![]()
令![]() , 得
, 得![]() .
.
因为直线![]() 与平面
与平面![]() 所成的角和此直线与平面
所成的角和此直线与平面![]() 所成的角相等,
所成的角相等,
所以![]() ,即
,即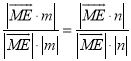 ,所以
,所以 ![]() ,
,
解得![]() ,或
,或![]() (舍). 综上所得:
(舍). 综上所得: ![]()

【题目】参加衡水中学数学选修课的同学,对某公司的一种产品销量与价格进行统计,得到如下数据和散点图:
定价 |
|
|
|
|
|
|
年销售 |
|
|
|
|
|
|
|
|
|
|
|
|
|
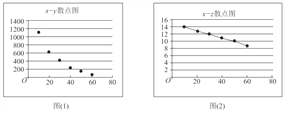
(参考数据:![]()
![]() )
)
(I)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(II)根据(I)的判断结果有数据,建立![]() 关于
关于![]() 的回归方程(方程中的系数均保留两位有效数字);
的回归方程(方程中的系数均保留两位有效数字);
(III)定价为多少元/![]() 时,年利润的预报值最大?
时,年利润的预报值最大?
附:对一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: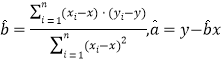 .
.