题目内容
已知圆 ,直线
,直线 。
。
(Ⅰ)求证:对 ,直线
,直线 与圆C总有两个不同交点.
与圆C总有两个不同交点.
(Ⅱ)设 与圆C交于不同两点A、B,求弦AB的中点M的轨迹方程.
与圆C交于不同两点A、B,求弦AB的中点M的轨迹方程.
 ,直线
,直线 。
。(Ⅰ)求证:对
 ,直线
,直线 与圆C总有两个不同交点.
与圆C总有两个不同交点.(Ⅱ)设
 与圆C交于不同两点A、B,求弦AB的中点M的轨迹方程.
与圆C交于不同两点A、B,求弦AB的中点M的轨迹方程.(1)见解析;(2)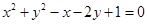 .
.
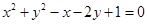 .
.本试题主要考查了直线与圆的位置关系的运用。
解:
(1)
解法一:
圆 的圆心为
的圆心为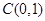 ,半径为
,半径为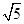 。
。
∴圆心C到直线 的距离
的距离 …………3分
…………3分
∴直线 与圆C相交,即直线
与圆C相交,即直线 与圆C总有两个不同交点;……………………6分
与圆C总有两个不同交点;……………………6分
解法二:
由 方程可得:m(x-1)-y+1=0,令x=1,则y=1
方程可得:m(x-1)-y+1=0,令x=1,则y=1
∴对于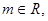
 恒过定点P(1,1),又12+(1-1)2<5 ………………………3分
恒过定点P(1,1),又12+(1-1)2<5 ………………………3分
∴P点在圆C内部
∴直线 与圆C相交,即直线
与圆C相交,即直线 与圆C总有两个不同交点; ……………………6分
与圆C总有两个不同交点; ……………………6分
(2)由(1)得 过定点P(1,1)
过定点P(1,1)
当M与P不重合时,连结CM、CP,则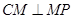 ,
,
∴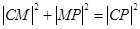 (或者kCM.kMP=-1)………………………………………9分
(或者kCM.kMP=-1)………………………………………9分
设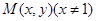 ,则
,则 ,
,
化简得: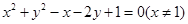
当M与P重合时,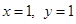 也满足上式。
也满足上式。
故弦AB中点的轨迹方程是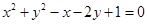 ……………………12分
……………………12分
解:
(1)
解法一:
圆
 的圆心为
的圆心为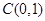 ,半径为
,半径为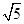 。
。∴圆心C到直线
 的距离
的距离 …………3分
…………3分∴直线
 与圆C相交,即直线
与圆C相交,即直线 与圆C总有两个不同交点;……………………6分
与圆C总有两个不同交点;……………………6分解法二:
由
 方程可得:m(x-1)-y+1=0,令x=1,则y=1
方程可得:m(x-1)-y+1=0,令x=1,则y=1∴对于
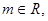
 恒过定点P(1,1),又12+(1-1)2<5 ………………………3分
恒过定点P(1,1),又12+(1-1)2<5 ………………………3分∴P点在圆C内部
∴直线
 与圆C相交,即直线
与圆C相交,即直线 与圆C总有两个不同交点; ……………………6分
与圆C总有两个不同交点; ……………………6分(2)由(1)得
 过定点P(1,1)
过定点P(1,1)当M与P不重合时,连结CM、CP,则
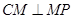 ,
,∴
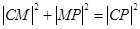 (或者kCM.kMP=-1)………………………………………9分
(或者kCM.kMP=-1)………………………………………9分设
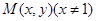 ,则
,则 ,
,化简得:
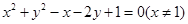
当M与P重合时,
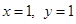 也满足上式。
也满足上式。故弦AB中点的轨迹方程是
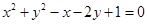 ……………………12分
……………………12分
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 的最小值为2,求直线AB的方程.
的最小值为2,求直线AB的方程.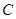 过点
过点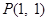 ,且与圆
,且与圆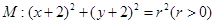 关于直线
关于直线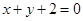 对称.
对称.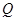 为圆
为圆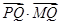 的最小值;
的最小值;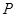 作两条相异直线分别与圆
作两条相异直线分别与圆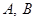 ,且直线
,且直线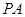 和
和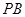 直线的倾斜角互补,
直线的倾斜角互补,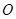 为坐标原点,试判断直线
为坐标原点,试判断直线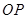 和
和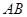 是否平行,并说明理由.
是否平行,并说明理由.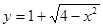 与直线
与直线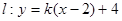 有两个交点时,实数
有两个交点时,实数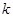 的取值范围是( )
的取值范围是( )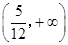

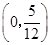
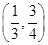
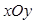 中,已知以
中,已知以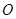 为圆心的圆与直线
为圆心的圆与直线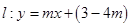
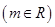 恒有公共点,且要求使圆
恒有公共点,且要求使圆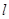 过定点,并指出定点坐标;
过定点,并指出定点坐标;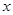 轴相交于
轴相交于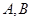 两点,圆内动点
两点,圆内动点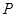 使
使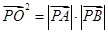 ,求
,求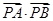 的取值范围.
的取值范围.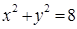 内有一点
内有一点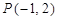 ,
, 为过点
为过点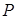 且倾斜角为
且倾斜角为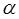 的弦,
的弦,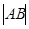 ;
; ,求点
,求点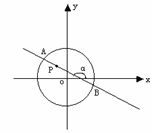
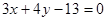 与圆
与圆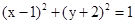 的位置关系是( )
的位置关系是( )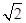 的点共有( )
的点共有( )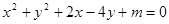 与直线
与直线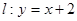 相切,且圆D与圆C关于直线
相切,且圆D与圆C关于直线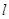 对称,则圆D的方程是___________。
对称,则圆D的方程是___________。