题目内容
圆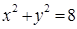 内有一点
内有一点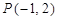 ,
, 为过点
为过点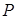 且倾斜角为
且倾斜角为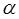 的弦,
的弦,
(1)当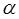 =1350时,求
=1350时,求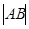 ;
;
(2)当弦 被点
被点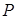 平分时,求出直线
平分时,求出直线 的方程;
的方程;
(3)设过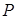 点的弦的中点为
点的弦的中点为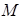 ,求点
,求点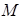 的轨迹方程.
的轨迹方程. 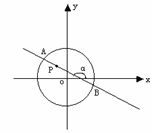
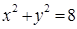 内有一点
内有一点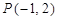 ,
, 为过点
为过点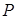 且倾斜角为
且倾斜角为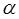 的弦,
的弦,(1)当
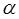 =1350时,求
=1350时,求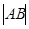 ;
;(2)当弦
 被点
被点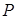 平分时,求出直线
平分时,求出直线 的方程;
的方程; (3)设过
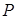 点的弦的中点为
点的弦的中点为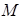 ,求点
,求点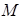 的轨迹方程.
的轨迹方程. 
(1)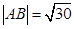
(2)
(3)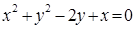
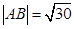
(2)

(3)
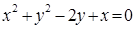
(1)由倾斜角可求出AB的斜率,然后求出直线方程,再求出圆心到直线的距离,利用 即可求出|AB|的值.
即可求出|AB|的值.
(2)由 ,即可求出AB的斜率,进而问题得解。
,即可求出AB的斜率,进而问题得解。
(3)那么点M在以OP为直径的圆上。因而问题得解。
解:(1)过点 做
做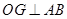 于
于 ,连结
,连结 ,当
,当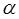 =1350时,直线
=1350时,直线 的斜率为-1,
的斜率为-1,
故直线 的方程x+y-1=0,∴OG=d=
的方程x+y-1=0,∴OG=d= ,
,
又∵r= ,∴
,∴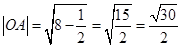 ,∴
,∴  ,
,
(2)当弦 被
被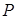 平分时,
平分时, ,此时KOP=
,此时KOP= ,
,
∴ 的点斜式方程为
的点斜式方程为 .
.
(3)设 的中点为
的中点为 ,
, 的斜率为K,
的斜率为K, ,则
,则 ,
,
消去K,得: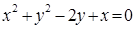 ,当
,当 的斜率K不存在时也成立,故过点
的斜率K不存在时也成立,故过点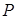 的弦的中点的轨迹方程为:
的弦的中点的轨迹方程为: 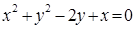 .
.
 即可求出|AB|的值.
即可求出|AB|的值.(2)由
 ,即可求出AB的斜率,进而问题得解。
,即可求出AB的斜率,进而问题得解。(3)那么点M在以OP为直径的圆上。因而问题得解。
解:(1)过点
 做
做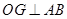 于
于 ,连结
,连结 ,当
,当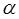 =1350时,直线
=1350时,直线 的斜率为-1,
的斜率为-1,故直线
 的方程x+y-1=0,∴OG=d=
的方程x+y-1=0,∴OG=d= ,
, 又∵r=
 ,∴
,∴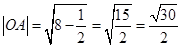 ,∴
,∴  ,
, (2)当弦
 被
被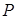 平分时,
平分时, ,此时KOP=
,此时KOP= ,
,∴
 的点斜式方程为
的点斜式方程为 .
. (3)设
 的中点为
的中点为 ,
, 的斜率为K,
的斜率为K, ,则
,则 ,
,消去K,得:
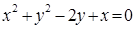 ,当
,当 的斜率K不存在时也成立,故过点
的斜率K不存在时也成立,故过点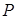 的弦的中点的轨迹方程为:
的弦的中点的轨迹方程为: 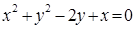 .
.
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ,点
,点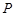 在直线
在直线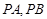 ,切点为
,切点为 .
. ,试求点
,试求点 三点的圆必过定点,并求出所有定点的坐标;
三点的圆必过定点,并求出所有定点的坐标; 长的最小值.
长的最小值. ,直线
,直线 。
。 ,直线
,直线 与圆C总有两个不同交点.
与圆C总有两个不同交点.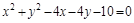 上的点到直线
上的点到直线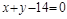 的最大距离与最小距离的差是( )
的最大距离与最小距离的差是( )
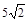
 与圆
与圆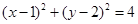 相交于
相交于 、
、 两点,且弦
两点,且弦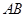 的长为
的长为 ,则
,则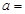 __________.
__________. 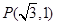 且与圆
且与圆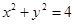 相切的直线方程 ___.
相切的直线方程 ___.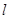 与圆C相交,则直线
与圆C相交,则直线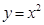
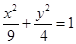
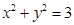
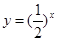
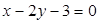 与圆
与圆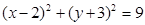 交于E、F两点,则弦长EF=
交于E、F两点,则弦长EF= 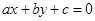 与圆
与圆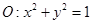 相交于A,B两点,且
相交于A,B两点,且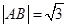 ,则
,则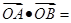 ________
________