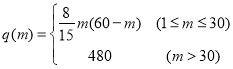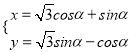Question

【题目】如图，在折线中，,,分别是的中点，若折线上满足条件的点至少有个，则实数的取值范围是___________.

Answer 1

【答案】

【解析】

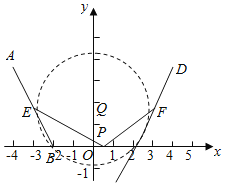
以BC的垂直平分线为y轴，以BC为x轴，建立如图所示的平面直角坐标系，分别表示各个点的坐标，设P（x，y），根据向量的数量积可得当k+9＞0时，点P的轨迹为以（0，）为圆心，以为半径的圆，结合图象，即可求出满足条件的点P至少有4个的k的取值范围．

解：以BC的垂直平分线为y轴，以BC为x轴，建立如图所示的平面直角坐标系，

∵AB＝BC＝CD＝4，∠ABC＝∠BCD＝120°，

∴B（﹣2.0），C（2，0），A（﹣4，2），D（4，2），

∵E、F分别是AB、CD的中点，

∴E（﹣3，），F（3，），

设P（x，y），﹣4≤x≤4，0≤y≤2，

∵，

∴（﹣3﹣x，（3﹣x，y）＝，

即，

当k+9＞0时，点P的轨迹为以（0，）为圆心，以为半径的圆，

当圆与直线DC相切时，此时圆的半径r，此时点有2个，

当圆经过点C时，此时圆的半径为r，此时点P有4个，

∵满足条件的点P至少有4个，结合图象可得，

∴k+9≤7，

解得k≤﹣2，

故实数k的取值范围为[，﹣2]，

故答案为：[，﹣2]