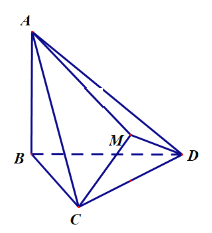
��Ŀ����
����Ŀ��ij��ݹ�˾��ij�еĻ���ת�����ģ����������ܻ����˷ּ�ϵͳ������߷ּ�Ч�ʺͽ��������ɱ�����֪����x̨�����˵��ܳɱ�Ϊ![]() ��Ԫ��
��Ԫ��

��1����ʹÿ̨�����˵�ƽ���ɱ���ͣ���Ӧ�����̨��
��2���ְ���1���е�������������ˣ���Ҫ����m�˽��ʼ����ڻ������ϣ������˽��ʼ��ʹ�ָ����������ɷּ���ͼ������ʵ��֪��ÿ̨�����˵���ƽ���ּ���Ϊ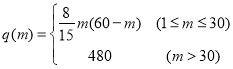 ������λ����������֪��ͳ���˹��ּ�ÿ��ÿ�յ�ƽ���ּ���Ϊ1200���������������˺���ƽ���ּ��������ʱ����������������������ǰ�������������ɼ��ٰٷ�֮����
������λ����������֪��ͳ���˹��ּ�ÿ��ÿ�յ�ƽ���ּ���Ϊ1200���������������˺���ƽ���ּ��������ʱ����������������������ǰ�������������ɼ��ٰٷ�֮����
���𰸡���1��300̨����2��![]() .
.
��������
��1�����ܳɱ�![]() ��Ԫ���ɵ�ÿ̨�����˵�ƽ���ɱ�
��Ԫ���ɵ�ÿ̨�����˵�ƽ���ɱ�![]() ��Ȼ�����û�������ʽ����ֵ��
��Ȼ�����û�������ʽ����ֵ��
��2�����������˺�ÿ̨�����˵���ƽ���ּ���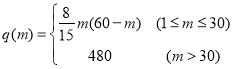 ���ֶ����300̨�����˵���ƽ���ּ��������ֵ�������������������ֵ����1200���ɵ÷ּ��������ֵʱ���贫ͳ�ּ���Ҫ��������𰸿���
���ֶ����300̨�����˵���ƽ���ּ��������ֵ�������������������ֵ����1200���ɵ÷ּ��������ֵʱ���贫ͳ�ּ���Ҫ��������𰸿���
�⣺��1�����ܳɱ�![]() ��Ԫ��
��Ԫ��
�ɵ�ÿ̨�����˵�ƽ���ɱ���
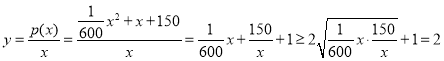 ��
��
���ҽ���![]() ����
����![]() ʱ����ʽ�Ⱥų�����
ʱ����ʽ�Ⱥų�����
����ʹÿ̨�����˵�ƽ���ɱ���ͣ�Ӧ��300̨��
��2�����������˺�ÿ̨�����˵���ƽ���ּ���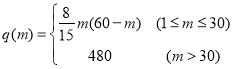 ��
��
��![]() ʱ��300̨�����˵���ƽ���ּ���Ϊ
ʱ��300̨�����˵���ƽ���ּ���Ϊ![]() ��
��
�൱![]() ʱ����ƽ���ּ��������ֵ144000��
ʱ����ƽ���ּ��������ֵ144000��
��![]() ʱ����ƽ���ּ���Ϊ480��300��144000��
ʱ����ƽ���ּ���Ϊ480��300��144000��
��300̨�����˵���ƽ���ּ��������ֵΪ144000����
����ͳ�˹��ּ�144000��������Ҫ����Ϊ![]() �ˣ�
�ˣ�
����ƽ���ּ��������ֵʱ����������������������ǰ�������������ɼ���![]() ��
��

����Ŀ��ijý��Ϊ����ϲ�����ֽ�Ŀ![]() �Ƿ�������Ա��йأ������ȡ��30�����Ժ�30��Ů�Թ��ڣ�������õȸ�����ͼ��ʾ��ͼ��
�Ƿ�������Ա��йأ������ȡ��30�����Ժ�30��Ů�Թ��ڣ�������õȸ�����ͼ��ʾ��ͼ��
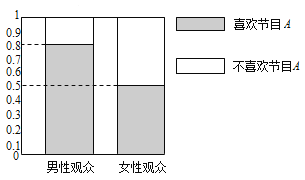
��1�����ݸõȸ�����ͼ���������![]() �����������ö����Լ���ķ����������ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊϲ�����ֽ�Ŀ
�����������ö����Լ���ķ����������ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊϲ�����ֽ�Ŀ![]() ������Ա��йأ�
������Ա��йأ�

��2�����Թ����а�ϲ����Ŀ![]() ����÷ֲ�����ķ�����ȡ5������һ�����飮����5������ѡ2������ǡ��1��ϲ����Ŀ
����÷ֲ�����ķ�����ȡ5������һ�����飮����5������ѡ2������ǡ��1��ϲ����Ŀ![]() ��1����ϲ����Ŀ
��1����ϲ����Ŀ![]() �ĸ��ʣ�
�ĸ��ʣ�
����
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
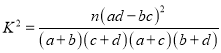 ��
��