Question

【题目】已知函数

（1）若对任意的，恒成立，求实数的取值范围；

（2）若的最小值为，求实数的值；

（3）若对任意实数、、，均存在以、、为三边边长的三角形，求实数的取值范围.

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）问题等价于4x+k2x+1＞0恒成立，分离出参数k后转化为求函数的最值问题即可；

（2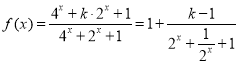），令，则，分k＞1，k＝1，k＜1三种情况进行讨论求出f（x）的最小值，令其为﹣3即可解得k值；

（3）由题意得f（x1）+f（x2）＞f（x3）对任意x1，x2，x3∈R恒成立，当k＝1时易判断；当k＞1，k＜1时转化为函数的最值问题解决即可，借助（2）问结论易求函数的最值.

（1）因为4x+2x+1＞0，所以f（x）＞0恒成立，等价于4x+k2x+1＞0恒成立，即k＞﹣2x﹣2﹣x恒成立，

因为﹣2x﹣2﹣x＝﹣（2x+2﹣x）≤﹣2，当且仅当2x＝2﹣x，即x＝0时取等号，所以k＞﹣2.

（2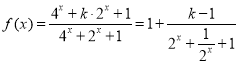），令，则，

当k＞1时，无最小值，舍去；

当k＝1时，y＝1，最小值不是﹣3，舍去；

当k＜1时，，最小值为，解得.

综上所述，k＝﹣11．

（3）由题意，f（x1）+f（x2）＞f（x3）对任意x1，x2，x3∈R恒成立．

当k＞1时，因，且，故，即1＜k≤4；

当k＝1时，f（x1）＝f（x2）＝f（x3）＝1，满足条件；

当k＜1时，，且，故，解得；

综上所述，