题目内容
【题目】已知几何体![]() 如图所示,其中
如图所示,其中![]() 两两互相垂直且
两两互相垂直且![]() ,且
,且![]() .
.
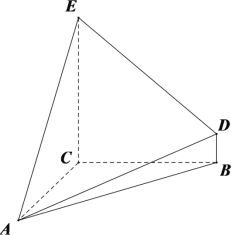
(1)求此几何体的体积;
(2)求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1) 首先证明![]() 平面
平面![]() ,再证明底面为梯形CEDB为梯形,利用四棱锥的体积公式可求出体积;
,再证明底面为梯形CEDB为梯形,利用四棱锥的体积公式可求出体积;
(2) 在线段EC上取点F,使得EF=BD=1,连接BF,AF,构造平行四边形EFBD,在![]() 中,运用余弦定理即可求得答案.
中,运用余弦定理即可求得答案.
(1)∵![]() 两两互相垂直,∴
两两互相垂直,∴![]() ,又∵
,又∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() ,故底面为梯形,所以几何体
,故底面为梯形,所以几何体![]() 为四棱锥,体积为
为四棱锥,体积为![]()
(2)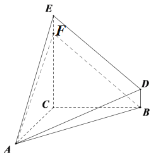
在线段EC上取点F,使得EF=BD=1,连接BF,AF,则四边形EFBD为平行四边形,DE//BF,则∠FBA即为异面直线![]() 与
与![]() 所成角,
所成角,![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
在![]() 中,由余弦定理可得
中,由余弦定理可得![]() ,即
,即![]() ,解得
,解得![]() ,即异面直线
,即异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】目前,中国有三分之二的城市面临“垃圾围城”的窘境. 我国的垃圾处理多采用填埋的方式,占用上万亩土地,并且严重污染环境. 垃圾分类把不易降解的物质分出来,减轻了土地的严重侵蚀,减少了土地流失. 2020年5月1日起,北京市将实行生活垃圾分类,分类标准为厨余垃圾、可回收物、有害垃圾和其它垃圾四类 .生活垃圾中有30%~40%可以回收利用,分出可回收垃圾既环保,又节约资源. 如:回收利用1吨废纸可再造出0.8吨好纸,可以挽救17棵大树,少用纯碱240千克,降低造纸的污染排放75%,节省造纸能源消耗40%~50%.
现调查了北京市5个小区12月份的生活垃圾投放情况,其中可回收物中废纸和塑料品的投放量如下表:
|
|
|
|
| |
废纸投放量(吨) | 5 | 5.1 | 5.2 | 4.8 | 4.9 |
塑料品投放量(吨) | 3.5 | 3.6 | 3.7 | 3.4 | 3.3 |
(Ⅰ)从![]() 这5个小区中任取1个小区,求该小区12月份的可回收物中,废纸投放量超过5吨且塑料品投放量超过3.5吨的概率;
这5个小区中任取1个小区,求该小区12月份的可回收物中,废纸投放量超过5吨且塑料品投放量超过3.5吨的概率;
(Ⅱ)从![]() 这5个小区中任取2个小区,记
这5个小区中任取2个小区,记![]() 为12月份投放的废纸可再造好纸超过4吨的小区个数,求
为12月份投放的废纸可再造好纸超过4吨的小区个数,求![]() 的分布列及期望.
的分布列及期望.